Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Один из простейших топологических инвариантов был открыт Гауссом. При исследованиях электрических и магнитных полей его заинтересовало, как могут быть связаны две замкнутые петли. Он изобрел коэффициент зацепления, который обозначает, сколько раз одна петля оборачивается вокруг другой. Если число зацеплений не равно 0, петли не могут быть разделены с помощью топологического преобразования. Однако данный инвариант не помогает достоверно определить, когда две соединенные петли невозможно разделить, ведь в некоторых случаях инвариант связывания равен 0, однако петли разделить невозможно.

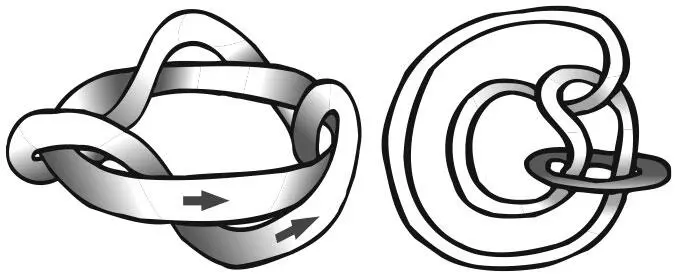
Слева: петли с коэффициентом зацепления 3. Справа: эти связи нельзя разделить топологически, хотя их коэффициент зацепления равен 0

Он даже составил аналитическую формулу для такого числа, взяв интеграл подходящей величины вдоль соответствующей кривой. Открытия Гаусса положили начало такой современной отрасли математики, как алгебраическая топология.

Теперь гипотеза Пуанкаре становится ее прямым следствием, поскольку условие, что все петли стягиваются, исключает семь геометрий, оставляя только геометрию постоянной положительной кривизны – трехмерной гиперсферы.

Альтернативный подход предлагает геометрия Римана. В 1982 г. Ричард Гамильтон открыл в этой области новые приемы, основанные на математических идеях, которые были использованы Альбертом Эйнштейном для обоснования общей теории относительности. По Эйнштейну, пространство-время можно считать изогнутым, а кривизна описывает силу притяжения. Она измеряется так называемым тензором кривизны, который имеет более простого родственника, известного как тензор Риччи (назван в честь его изобретателя Грегорио Риччи-Курбастро). Изменения в геометрии Вселенной, связанные со временем, описываются уравнениями Эйнштейна, где говорится, что кривизна пропорциональна силе тензора. В результате гравитационные искривления Вселенной стараются со временем выпрямиться, и уравнения Эйнштейна количественно описывают эту идею.

Тот же фокус можно проделать и с использованием версии кривизны Риччи, и мы получим ту же модель поведения: поверхность, подчиняющаяся уравнениям для потока Риччи, естественным путем стремится к упрощению своей геометрии, более справедливо распределяя свою кривизну. Гамильтон показал, что гипотеза Пуанкаре для двумерного пространства может быть доказана с помощью потока Риччи – на основании того, что поверхность, на которой все петли стягиваются, упрощает саму себя по мере того, как следует потоку Риччи, так что в конце получается идеальная сфера. Гамильтон также предложил обобщить этот подход для трехмерного пространства и даже добился определенного успеха в своих исследованиях, пока не натолкнулся на ряд трудностей.

В 2002 г. Григорий Перельман произвел сенсацию, выложив несколько своих статей на arXiv – сайте, созданном физиками и математиками для нерецензируемых публикаций и подчас даже еще не законченных исследований. Так ученые могли избежать проволочек из-за реферирования, неизбежных при официальной публикации своих открытий. Ранее этой же цели служили периодически издававшиеся на бумаге неофициальные препринты. На первый взгляд статьи Перельмана посвящены потоку Риччи, но на самом деле становится понятно, что если открытия автора верны, они послужат доказательством гипотезы геометризации, которую сформулировал Пуанкаре.

Основную идею предложил еще Гамильтон. Возьмите произвольное трехмерное многообразие, снабдите его понятием расстояния так, чтобы можно было применить поток Риччи, и позвольте многообразию следовать потоку, упрощая себя. Главным возможным осложнением становятся особенности, которые возникнут там, где многообразие сжимается, когда оно перестает быть гладким. При сингулярности предложенный метод не работал. Свежая идея состояла в том, чтобы устранить эти сингулярности, тем самым открыть появившиеся отверстия и удалить все препятствия для потока. Если многообразию удастся упростить самое себя полностью после того, как появилось только конечное число сигулярностей, каждая часть будет поддерживать только одну из восьми геометрий, и операции, обратные вырезанию (хирургия, или перестройка Морса), покажут нам, как снова склеить эти части в целое и восстановить многообразие.