Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

О возможности соединения такого рода первым заговорил Мёбиус, чья лента имела одну сторону и один край. Клейн пошел дальше, концептуально склеив в круглый диск края ленты Мёбиуса, чтобы избавиться от края. Получившаяся поверхность, в шутку прозванная бутылкой Клейна , имеет только одну сторону и вовсе не имеет краев. Если мы попытаемся изобразить ее в привычном трехмерном пространстве, ей придется пройти себя насквозь. Но в качестве абстрактной поверхности (или поверхности, помещенной в четырехмерное пространство) она не пронзит себя.

Теперь теорему о торах с g отверстиями можно переформулировать так: любая ориентируемая поверхность (или конечное пространство без границ) топологически эквивалента сфере с g дополнительными отверстиями (где g может быть равно 0). Есть соответствующая классификация и для неориентируемых (односторонних) поверхностей: они могут быть образованы поверхностью под названием проективная плоскость путем добавления g отверстий. Бутылка Клейна как раз и является проективной поверхностью с одним отверстием.

Комбинация этих двух результатов называется теоремой о классификации поверхностей. Она позволяет описать в топологическом эквиваленте любую возможную поверхность (или конечное пространство без границ). С доказательством этой теоремы топология двумерных пространств – поверхностей – может считаться вполне изученной. Это, конечно, не значит, что на любой вопрос о поверхностях теперь легко найти ответ, но по крайней мере это дает хороший задел для исследований новых сложных проблем. В любом случае, теорема о классификации поверхностей – чрезвычайно важный инструмент двумерной топологии.

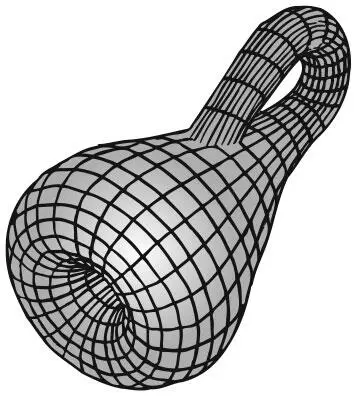
Бутылка Клейна. Видимое самопересечение – не более чем иллюзия, возникающая из-за трехмерности изображения

Анри Пуанкаре родился во французском Нанси. Его отец Леон был профессором медицины в Университете Нанси, его мать звали Эжени Лануа. Его кузен, Раймон Пуанкаре, стал французским премьер-министром и даже занимал пост президента страны во время Первой мировой войны. Анри отлично успевал по всем предметам в школе, особенно выделяясь в математике. Прекрасная память и способность легко представить себе объемное изображение даже самой сложной формы помогали компенсировать его слабое зрение: ученик едва различал классную доску, не говоря уж о том, что на ней было написано.

Его первой должностьюбыл пост преподавателя в университете города Кан в 1879 г., но уже в 1881 г. он удостоился гораздо более денежного и престижного места в Парижском университете. Там он стал одним из ведущих математиков своего времени. Он работал систематически – каждый день по четыре часа, разбитых на два двухчасовых промежутка, утром и вечером. Но полет его мысли не поддавался столь строгой организации, и зачастую он принимался писать статью, не имея даже представления о том, к чему приведет его новое исследование и как оно закончится. Его отличала высочайшая интуиция, и лучшие идеи приходили часто в те моменты, когда он размышлял о чем-то постороннем.

Среди своих современников он, несомненно, был самым выдающимся математиком, сделавшим немало важных открытий в теории комплексного переменного, дифференциальных уравнений, неевклидовой геометрии и топологии – которую отчасти и создал. Он много занимался прикладными исследованиями в области электричества, сопротивления материалов, оптики, термодинамики, теории относительности, квантовой теории, астрономии и космологии.

Он завоевал главный призв конкурсе, объявленном в 1887 г. королем Швеции и Норвегии Оскаром II. Темой была объявлена «задача трех тел» – исследование движения гравитационно взаимодействующих трех тел. В поданную на конкурс работу закралась ошибка, которую удалось быстро исправить. В результате были открыты возможности того, что сейчас известно под названием «хаос»: беспорядочное, непредсказуемое движение в системе, подчиняющейся детерминированным законам. Также он опубликовал несколько чрезвычайно популярных и известных книг: «Наука и гипотеза» (1901), «Ценность науки» (1905), «Наука и метод» (1908).