Несколькими годами позже Гильберт расширил свои результаты и представил в журнал новую статью. Клейн принял ее, охарактеризовав как «важнейшую работу по общей алгебре, которую Annalen когда-либо публиковали». Что же касается Гильберта, то он теперь сделал все, что намеревался сделать в этой области. «Я определенно оставлю область инвариантов», – написал он Минковскому. И оставил.
* * *
Доведя до совершенства теорию инвариантов – эта область исследований, по существу, заглохла после того, как с ней поработал Гильберт, и оживилась лишь много лет спустя в еще более общем контексте, причем тогда возродился интерес одновременно и к вычислениям, и к понятиям, – Гильберт нашел для себя новую область приложения сил. В 1893 г. он начал новый проект – «Отчет о числах» ( Zahlbericht ). Дело в том, что Немецкое математическое общество предложило ему исследовать крупную область теории чисел – ту область, где рассматриваются алгебраические числа, то есть комплексные числа, удовлетворяющие полиномиальному уравнению с рациональными (или, что эквивалентно, целыми) коэффициентами. Примером алгебраического числа может служить 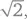 удовлетворяющий уравнению x 2–2 = 0; еще один пример – мнимое число i, удовлетворяющее уравнению x 2+ 1 = 0. Как отмечено в главе 16, комплексные числа, которые не являются алгебраическими, называют трансцендентными; примеры таких чисел включают числа π и e, хотя это свойство трудно доказать, и долгое время вопрос оставался открытым. Трансцендентность e доказал Шарль Эрмит в 1873 г., а с трансцендентностью π разобрался Линдеман в 1882 г.
удовлетворяющий уравнению x 2–2 = 0; еще один пример – мнимое число i, удовлетворяющее уравнению x 2+ 1 = 0. Как отмечено в главе 16, комплексные числа, которые не являются алгебраическими, называют трансцендентными; примеры таких чисел включают числа π и e, хотя это свойство трудно доказать, и долгое время вопрос оставался открытым. Трансцендентность e доказал Шарль Эрмит в 1873 г., а с трансцендентностью π разобрался Линдеман в 1882 г.
Основную роль алгебраические числа играют в теории чисел. Эйлер неявно использовал некоторые их свойства, к примеру при доказательстве Великой теоремы Ферма для кубов, но систематическое их изучение начал Гаусс. Пытаясь обобщить свой закон квадратичной взаимности на степени выше двойки, он открыл красивое расширение его на четвертые степени, основанное на алгебраических числах вида a + i b , где a и b – целые. Эта система «Гауссовых целых чисел» обладает многими особыми свойствами, в частности, имеет собственный аналог простых чисел и к нему собственную теорему о единственности разложения. Кроме того, Гаусс использовал алгебраические числа, имеющие отношение к корням единицы, при построении правильного семнадцатиугольника.
В главе 6, в связи с Великой теоремой Ферма, мы говорили о том, как использовал алгебраические числа Куммер и какое он предложил понятие идеальных чисел. Дедекинд упростил эту идею, переформулировав ее в терминах особых множеств алгебраических чисел, которые он назвал идеалами. После Куммера теория алгебраических чисел рванула вперед с помощью и при содействии теории уравнений Галуа и так же активно развивающейся абстрактной алгебры (глава 20). Фразу «алгебраическая теория чисел» можно интерпретировать двояко: это может быть и алгебраический подход к теории чисел, и теория алгебраических чисел. Теперь же оба значения сходились к одному и тому же, и именно в этом Немецкое математическое общество просило Гильберта разобраться. Он, что характерно, пошел намного дальше. Он задался вопросом, которым испокон веков задаются математики, столкнувшиеся с большим массивом интересных, но неорганизованных результатов: «Да, конечно, но о чем это на самом деле ?» Поиск ответов на этот вопрос позволил ему сформулировать и доказать множество новых теорем.
Все время работы над «Отчетом о числах» Гильберт вел обширную переписку на эту тему с Минковским – иногда даже слишком обширную, так что временами Гильберт чувствовал настоящее отчаяние; ему начинало казаться, что работа никогда не будет закончена в виде, который удовлетворил бы его взыскательного друга. Однако в конечном итоге отчет был опубликован. В нем были сформулированы и доказаны общие аналоги квадратичной взаимности, образовавшие основу того, что мы сегодня называем теорией полей классов – это до сих пор активно развивающаяся, хотя и весьма сложная технически понятийная основа для теории алгебраических чисел. В предисловии к «Отчетам» говорится:
Таким образом, мы видим, как далеко арифметика – королева математики – зашла в захвате обширных областей алгебры и теории функций, чтобы стать их лидером… Следует заключить, если я не ошибаюсь, что прежде всего современное развитие теоретической математики происходит под знаменем числа.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

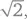 удовлетворяющий уравнению x 2–2 = 0; еще один пример – мнимое число i, удовлетворяющее уравнению x 2+ 1 = 0. Как отмечено в главе 16, комплексные числа, которые не являются алгебраическими, называют трансцендентными; примеры таких чисел включают числа π и e, хотя это свойство трудно доказать, и долгое время вопрос оставался открытым. Трансцендентность e доказал Шарль Эрмит в 1873 г., а с трансцендентностью π разобрался Линдеман в 1882 г.
удовлетворяющий уравнению x 2–2 = 0; еще один пример – мнимое число i, удовлетворяющее уравнению x 2+ 1 = 0. Как отмечено в главе 16, комплексные числа, которые не являются алгебраическими, называют трансцендентными; примеры таких чисел включают числа π и e, хотя это свойство трудно доказать, и долгое время вопрос оставался открытым. Трансцендентность e доказал Шарль Эрмит в 1873 г., а с трансцендентностью π разобрался Линдеман в 1882 г.










