Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

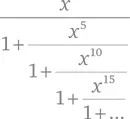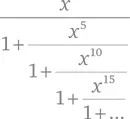
которое было написано на последней странице его письма в составе по-настоящему жуткой, но правильной формулы. Некоторые из своих формул Рамануджан применял в теории чисел, где его особо интересовала аналитическая теория чисел, которая ищет простые приближения для таких величин, как число простых чисел до заданного предела – теорема о простых Гаусса (глава 10) – или среднее число делителей у заданного числа.

Его публикации во время пребывания в Кембридже готовились под влиянием общения с Харди и были написаны в традиционном стиле, со строгими доказательствами. Результаты, записанные в его блокнотах, выглядят совершенно иначе. Поскольку он был самоучкой, представления о доказательстве у него были совсем не строгие. Для Рамануджана было достаточно, если при помощи численных данных пополам с формальными рассуждениями он мог получить правдоподобный вывод – и при этом интуиция говорила ему, что ответ верен. Как правило, его результаты были верны, но в доказательствах часто имелись пробелы. Иногда эти пробелы мог заполнить любой компетентный математик, а иногда для этого требовались нестандартные аргументы. В редких случаях в его результатах обнаруживалась ошибка. Берндт утверждает, что, если бы Рамануджан «мыслил как хорошо подготовленный математик, он не стал бы записывать многие из тех формул, которые он, по собственному мнению, доказал» и математика от этого серьезно пострадала бы.

Хорошим примером может служить результат, который Рамануджан называл своей «мастер-формулой» [28] Мастер-формула Рамануджана гласит, что если есть комплекснозначная функция, то где Г( s ) есть Эйлерова гамма-функция. – Прим. авт. . Его доказательство включает в себя разложения в ряд, смену порядка суммирования и интегрирования и другие аналогичные приемы. Поскольку он использует при этом бесконечные процессы, каждый его шаг сопряжен с опасностью. Величайшие аналитики почти весь XIX век разбирались, когда подобные процедуры допустимы. Условия, которые, по Рамануджану, делают его формулу верной, чрезвычайно недостаточны. Тем не менее почти все результаты, которые он выводит из своей мастер-формулы, верны.

Часть самых поразительных работ Рамануджана относится к теории разбиений – одного из разделов теории чисел. Взяв некоторое натуральное число, мы спрашиваем, сколькими способами его можно разбить на слагаемые, то есть записать в виде суммы меньших натуральных чисел. К примеру, число 5 можно разбить на слагаемые семью разными способами:

5 4 + 1 3 + 2 3 + 1 + 1 2 + 2 + 1 2 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1

Следовательно, число разбиений числа 5 составляет p (5) = 7. Величина p ( n ) стремительно растет с ростом n . К примеру, p (50) = 204 226, а p (200) равно внушительному 3 972 999 029 388. Простой формулы для p ( n ) не существует. Однако можно поискать приближенную формулу, задающую общий порядок величины p ( n ). Это задача аналитической теории чисел, причем одна из наиболее неподатливых. В 1918 г. Харди и Рамануджан преодолели технические трудности и вывели-таки приближенную формулу – довольно сложный ряд, включающий в себя комплексные корни 24-й степени из единицы. Затем они обнаружили, что при n = 200 одно только первое слагаемое дает первые 6 значащих цифр точного значения. Добавив к нему еще всего лишь 7 слагаемых, они получили число 3 972 999 029 388,004, целая часть которого равна точной величине. Они заметили, что этот результат «позволяет однозначно предположить, что можно получить формулу для p ( n ), которая не только будет выявлять его порядок величины и структуру, но и может быть использована для вычисления его точной величины для любого n », после чего доказали именно это. Должно быть, это один из редчайших случаев, когда поиск приближенной формулы в результате привел к точной формуле.

Кроме того, Рамануджан нашел в разбиениях кое-какие замечательные закономерности. В 1919 г. он доказал, что p (5 k + 4) всегда делится на 5, а p (7 k + 5) всегда делится на 7. В 1920 г. он заявил еще несколько аналогичных результатов: к примеру, p (11 k + 6) всегда делится на 11; p (25 k + 24) делится на 25; p (49 k + 19), p (49 k + 33), p (49 k + 40) и p (49 k + 47) делятся на 49; p (121 k + 116) делится на 121. Обратите внимание: 25 = 5 2, 49 = 7 2, а 121 = 11 2. Рамануджан говорил, что, насколько он может судить, такие формулы существуют только для делителей вида 5 a 7 b 11 c , но это оказалось неверным. Артур Аткин обнаружил, что p (17303 k + 237) делится на 13, а в 2000 г. Кен Оно доказал, что соответствия такого рода существуют для всех простых модулей. Еще через год он и Скотт Алгрен доказали, что они существуют для всех модулей, не кратных 6.