Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

Он был не только выдающимся исследователем, но и видным преподавателем, принимал участие в образовательных проектах для средней школы, за что был избран президентом Математической ассоциации Америки. Среди его учеников — нобелевский лауреат Джон Нэш.

Существует четыре возможных решения: (А, А), (А, Б), (Б, А) и (Б, Б). Первая координата в каждой паре — стратегия Р1, вторая — стратегия Р2. Возможные исходы можно представить таблицей:

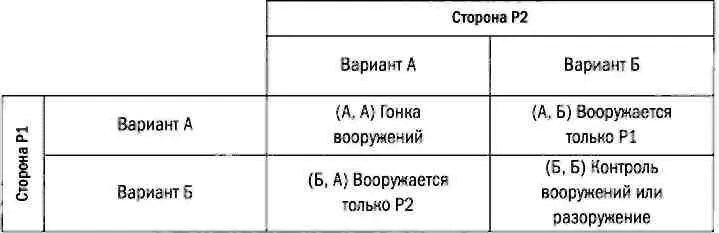
Пересечениям возможных стратегий можно присвоить значения (в терминах теории игр — платежи), учитывая, что для каждого игрока они будут отличаться и в каждой ячейке будет два числа: одно означает выгоду Р1, второе — выгоду Р2. Получим следующую платежную матрицу:

Если понимать эти числа как выигрыши, то дилемма очевидна. Что нужно делать Р1? Для любого из вариантов, доступных Р2, для Р1 будет выгоднее вооружаться. Если Р2 выберет вариант А, Р1 выиграет 2 в случае вооружения и 0 в противном случае. Если Р2 выберет вариант Б, Р1 выиграет 5, если будет вооружаться, и 4 в противном случае. Так как матрица симметричная, для Р2 можно привести аналогичные рассуждения. Для любой из двух стратегий Р1 наибольший выигрыш Р2 принесет выбор в пользу вооружения. Говорят, что решение (А, А), означающее, что обе стороны вооружаются и получают выгоду в 2, является равновесным некооперативным решением, к которому стремятся обе стороны.

Однако для каждого из участников будет лучше, если противник будет разоружаться (выигрыш возрастет). Кроме того, наибольший совокупный выигрыш достигается тогда, когда разоружаются обе стороны. Следовательно, если оппоненты не будут сотрудничать, наилучший совокупный результат (4, 4) невозможен. Но если одна из сторон сделает выбор в пользу сотрудничества, при этом не зная о действиях другой стороны, то подвергнется большому риску: если оппонент не будет сотрудничать, выигрыш окажется наименьшим. Поэтому уверенность становится важнейшим элементом игры: без нее каждая сторона будет пытаться защитить себя от возможного отказа сотрудничать со стороны противника.

В реальных условиях, не столь острых, как в нашем примере, можно достичь ситуации, когда сотрудничество станет возможным. Обычно игра повторяется несколько раз, и на первый план выходят такие понятия, как репутация и уверенность, которые могут существенно повлиять на ход игры, и игроки смогут узнать о взаимной выгоде. В нашем примере разоружение очевидно имеет многие преимущества по сравнению с гонкой вооружений, которая может привести к полному разорению. Несмотря на это, сотрудничество сложно и достижимо лишь в долгосрочной перспективе.

Хотя дилемма заключенного является частью теории игр, проблема, лежащая в основе этой задачи, рассматривалась задолго до появления этой теории. Английский философ Томас Гоббс (1588—1679), автор «Левиафана», рассуждая об абсолютизме, анализирует развитие общества и рассматривает проблему, схожую с дилеммой заключенного. Гоббс писал, что изначально общество пребывает в анархии, где есть место только конкуренции. Чтобы сотрудничество стало возможным, нужно наложить ограничения и обеспечить их выполнение. Гоббс рассматривал общественный договор как результат сотрудничества и полагал, что общество должно подчиниться правительству, так как независимые решения, предполагающие сотрудничество или соперничество, не должны приниматься отдельными людьми.

Ситуации, напоминающие дилемму заключенного, также можно встретить в деловом мире. На конкурентном рынке часто случается, что конкуренты отвергают практический подход, будучи убежденными, что со временем подобное поведение окажется выгодным для всех, в том числе и для них самих. Так, соглашение книжных магазинов не предоставлять скидок выше определенного процента (например, 10%) или решение профсоюза закрывать магазины в определенный час (например, в 20:00) направлены на рост продаж. Все участники знают, что, если хотя бы один из них не выполнит соглашение, его нарушат и остальные и никто не получит выгоды; напротив, расходы лишь возрастут.

Роберт Аксельрод, преподаватель политологии в университете Мичигана, математик и доктор политических наук, является экспертом в кооперативных задачах и специалистом по играм, подобным дилемме заключенного. Среди его трудов выделяется «Эволюция сотрудничества» (The Evolution of Cooperation), где изучается развитие сотрудничества как явления. Основная мысль книги такова: стратегии, используемые людьми, эволюционируют в сторону более эффективных, где обязательным элементом является сотрудничество. Говоря о дилемме заключенного, Аксельрод замечает, что если игра проводится один раз, то нельзя узнать поведение соперника, наградить его за сотрудничество или наказать за соперничество, поэтому нужно думать о краткосрочных результатах. Напротив, если игра повторяется несколько раз, то стратегии могут основываться на предыдущих взаимодействиях и их основным принципом будет взаимность: если противник часто сотрудничал с нами, будет лучше, если мы тоже продолжим сотрудничество, но если попыток сотрудничества не было, то нам не стоит и пытаться этого делать. Так как никому не удавалось определить оптимальную стратегию, Аксельрод организовал турнир между экспертами по теории игр, чтобы изучить, как они будут действовать и как будут пытаться скрыть действенные стратегии. В результате оказалось, что лучшей из всех стратегий оказалась простейшая, так называемая «око за око». Нужно начинать с сотрудничества (и никогда не отказываться от него первым), а затем повторять стратегию, выбранную соперником на прошлом ходу. Если противник сотрудничал с нами, стоит продолжать сотрудничество, но если он отказался это сделать, то нужно сразу выразить несогласие с этим.