Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

Можно сказать, что все множество ситуаций, изучаемых в теории игр, можно разделить на две полярные группы: игры с нулевой суммой, основанные на чистом соперничестве, и игры, основанные на чистом сотрудничестве. И те и другие легко решить, по крайней мере в теории. Игры, основанные на чистом соперничестве, рассматривались в прошлой главе. Аналогично можно анализировать ситуации, основанные на чистом сотрудничестве: действия пилота раллийного автомобиля и его штурмана, действия партнеров в танце, действия пилота самолета и диспетчера — это всё примеры ситуаций, где оба игрока имеют одну цель, и решение состоит в том, чтобы объединить усилия (эффективно координировать ходы).

Прочие игры для двух лиц, о которых рассказывается в этой главе, находятся между этими двумя крайностями. Такие игры сложнее, поскольку интересы игроков частично противоположны, а частично совпадают, хотя на первый взгляд кажется, что это не так. Представим, например, продавца квартиры и возможного покупателя. Оба заинтересованы в заключении сделки (в сотрудничестве), но не могут сойтись в цене (конфликт). Можно также рассмотреть пример слияния двух компаний или противостояние двух стран, которые ведут войну. Во всех подобных случаях большинство стратегий подразумевают конфликт, но есть возможность прийти к соглашению или подписать пакт, который частично устроит обе стороны: можно заключить перемирие или соглашение о неиспользовании ядерного оружия.

В 1944 году была опубликована работа фон Неймана и Моргенштерна «Теория игр и экономическое поведение», в которой излагался алгоритм поиска оптимальных решений в играх с нулевой суммой для двух лиц. Именно это событие считается отправной точкой теории игр. Основным предметом исследований новой теории стали кооперативные игры и анализ оптимальных стратегий в случаях, когда оппоненты могут прийти к соглашению относительно выбранных стратегий.

В 50-е годы XX века в теории игр произошел заметный прорыв. Появились первые исследования дилеммы заключенного, Джон Нэш определил понятие оптимальной стратегии для игр со множеством игроков, когда оптимальную стратегию нельзя определить заранее (подобная ситуация известна как равновесие Нэша). Этот алгоритм применим для некооперативных игр, но может быть расширен и для кооперативных. В это же время теория игр впервые начала применяться в других областях помимо экономики, например, в философии и политологии. Позднее, уже в 1970-е годы, теория игр начала применяться в биологии в основном благодаря работам Джона Мейнарда Смита, который ввел понятие эволюционно стабильной стратегии.

Фотография Оскара Моргенштерна, который вместе с Джоном фон Нейманом является создателем теории игр.

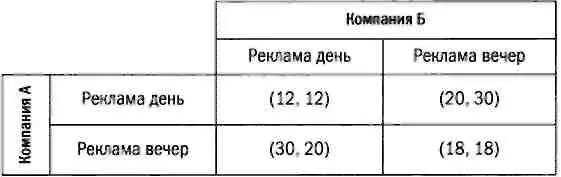
Чтобы показать разницу между играми с нулевой и с ненулевой суммой, рассмотрим ситуацию, связанную с распространением рекламы. Две компании, А и Б, хотят прорекламировать свою продукцию. В обе компании поступает предложение от телеканала: рекламу можно показать днем (когда ее увидят 40% телезрителей) или вечером (тогда ее увидят 60% зрителей), причем можно выбрать только один из предложенных вариантов. Известно, что дневная и вечерняя аудитории не пересекаются. Если обе компании закажут рекламу на одно и то же время, то их продукцию купят 30% зрителей, включивших телевизор в это время, и никто из тех, кто смотрел телевизор в другое время. Если же компании закажут рекламу на разное время, то охватят 50% аудитории, которая в тот момент находилась у экранов. Какое решение оптимально для каждой компании? Будет лучше проконсультироваться с другой компанией или скрыть свои намерения?

Эту игру можно выразить в виде платежной матрицы, значения которой будут соответствовать доле аудитории. Однако в этом случае в каждую ячейку таблицы нельзя поместить какое-то одно значение, так как выигрыш одной компании не равен проигрышу другой и каждая компания будет иметь свою выгоду. По этой причине элементами матрицы будут пары значений. Первое число в каждой паре — выгода компании А, второе — выгода компании Б в зависимости от стратегий, выбранных обеими компаниями.