Ласло Мерё - Логика чудес. Осмысление событий редких, очень редких и редких до невозможности

Фактор Мандельброта — очень изящная математическая концепция. Теоретически он представляет собой точную меру «дикости» той или иной сети. К сожалению, рассчитать этот фактор для каждой конкретной сети очень трудно, потому что это вычисление требует огромного объема данных, а в реально встречающихся сетях данные могут быть неточными и противоречивыми. Тем не менее некоторые исследователи берутся за решение этой задачи, и в нескольких недавних научных работах описываются попытки оценки фактора Мандельброта для безмасштабных сетей реального мира. В большинстве таких статей приводятся оценки какого-нибудь другого параметра сети, который можно использовать для определения фактора Мандельброта.

Некоторые из этих результатов представлены в верхней части таблицы 1 на с. 198. Поскольку реальные значения фактора Мандельброта невозможно привести с высокой точностью, я не даю никаких конкретных численных оценок. Вместо этого я разбил сети на три группы: те, у которых фактор Мандельброта существенно меньше 1 (слабо хаотичные), те, у которых он близок к 1 (пограничное состояние с точки зрения наличия или отсутствия стандартного отклонения), и те, у которых этот фактор существенно превышает 1 (следовательно, у них даже в теории не существует стандартного отклонения). Так как оценки приблизительны, принадлежность сетей к этим группам не следует считать абсолютно точной. Тем не менее эта таблица дает хорошее представление о степени дикости хаоса в различных областях.

В нижней части таблицы я перечислил несколько явлений, не относящихся к сетям, но имеющим приблизительно масштабно-инвариантное распределение, — как это было с озерами в начале этой главы. Эти примеры показывают, что масштабная инвариантность проявляется не только в структуре сетей и завораживающих геометрических свойствах фракталов, но и во многих других формах. Из таблицы можно увидеть, насколько хаотичными могут быть некоторые явления в биологии, социальных взаимодействиях, технике и экономике. Например, биологическая пищевая цепочка не относится к Тихонии, но тем не менее обладает очень слабой хаотичностью. Сеть сексуальных связей находится в противоположном конце спектра. Она даже более хаотична, чем могло бы предположить большинство людей, — хотя, если исключить из рассмотрения случаи проституции, а также сатириаза и нимфомании, оставшаяся сеть хорошо укладывается во вторую группу, что соответствует достаточно высокому уровню хаотичности.

Таблица 1.Порядок величины фактора Мандельброта для некоторых сетей и явлений

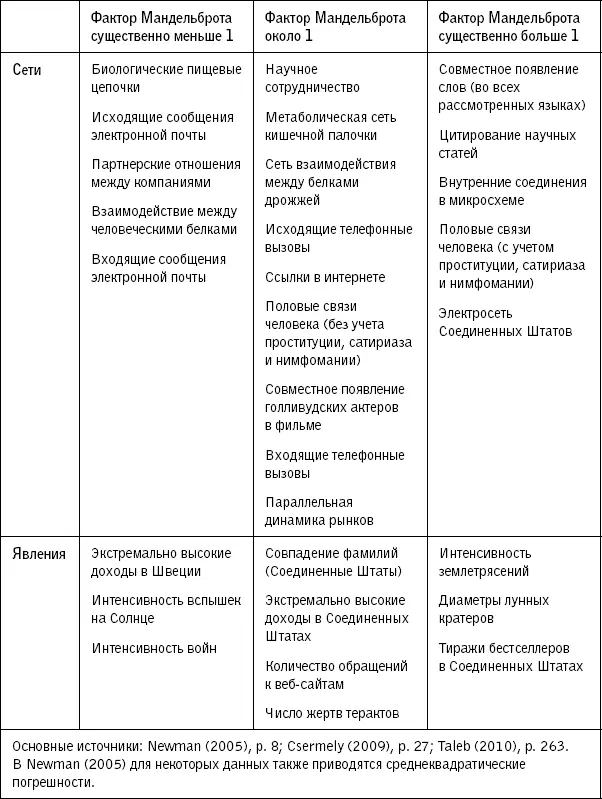
Возможно, покажется удивительным, что факторы Мандельброта природных и человеческих сетей часто близки к 1. Стоит отметить, что принцип Парето (или правило 80/20), который я описал в главе 5, справедлив при факторе Мандельброта, равном 1 (или чуть меньше). Следовательно, имеющиеся у нас сейчас результаты лишний раз подтверждают правило 80/20 и помогают определить область его действия.

Что касается случаев, в которых фактор Мандельброта больше 1, то несколько сетей и явлений, которые мы раньше считали — исходя из веских теоретических оснований — масштабно-инвариантными, оказываются в категории феноменов еще более экстремальных. Например, область человеческих талантов справедливо отнести не к умеренно дикому миру, но к миру истинно дикому, и для ее описания мы используем распределение Коши. Талант может проявляться множеством поразительно разных образов, и диапазон талантливости конкретных людей может быть на удивление широким.

Такого же рода дикость обнаруживается в списках адресатов электронной почты; они образуют сеть даже не масштабно-инвариантную, а еще более хаотичную. Это особенно интересно, потому что из нашей таблицы видно, что сам обмен сообщениями электронной почты оказывается безмасштабным, и его фактор Мандельброта не особенно велик. Гораздо более хаотичная сеть образуется за счет адресатов, с которыми мы на самом деле не переписываемся, но которые каким-то образом оказываются в нашей адресной книге. Эта более дикая сеть не фигурирует в таблице. В число других явлений, слишком диких для классификации в этой таблице, входят масштабы лесных пожаров и численность видов птиц в Америке. Дикость их распределений оказывается выше безмасштабного уровня [102] Newman (2005). .