Ласло Мерё - Логика чудес. Осмысление событий редких, очень редких и редких до невозможности

Чем меньше фактор Мандельброта безмасштабной сети, тем более распределение связей между ее вершинами приближается к распределению Гаусса. Другими словами, малые значения фактора Мандельброта соответствуют более тихим сетям. Тем не менее безмасштабная сеть никогда не бывает настолько тихой, чтобы стать предсказуемой; она всегда остается хаотичной. Тихая безмасштабная сеть описывает сравнительно тихий хаос. Верно и обратное: чем больше фактор Мандельброта сети, тем ближе распределение связей между ее вершинами оказывается к распределению Коши. Это означает, что в более диких сетях узлы крупнее, чем в более тихих.

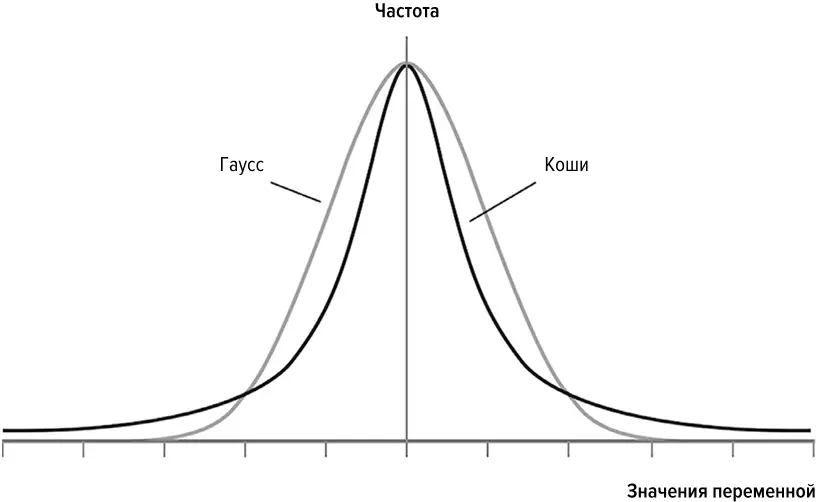
Илл. 21.Сравнение распределений Гаусса и Коши

(График Йожефа Бенце)

Переход между распределениями Гаусса и Коши становится особенно интересным, если попытаться выяснить, имеет ли промежуточное распределение стандартное отклонение. Из того, о чем мы говорили раньше, мы помним, что у распределения Гаусса есть стандартное отклонение, а у распределения Коши его нет. Математически доказано, что у масштабно-инвариантных распределений, фактор Мандельброта которых меньше 1, есть хорошо определенное стандартное отклонение, а те, фактор Мандельброта которых больше или равен 1, его не имеют [101] Для читателей, более искушенных в математике, уточним, что фактор Мандельброта, равный 1, соответствует показателю Парето, равному 2. . Это показывает, что весь диапазон от тихого до дикого действительно занимают безмасштабные сети. Тем не менее всякая безмасштабная сеть хаотична.

В главе 7, которая называлась «Математика непредсказуемого», я дал очень узкое определение хаоса и отметил, что существуют объекты даже более хаотичные, чем те, которые удовлетворяют нашему определению хаоса. То же можно сказать и о безмасштабных сетях. Если, например, число соединений, исходящих из каждой вершины, определяет наша снайпер Фиби, то сеть уже не будет ни безмасштабной, ни хаотической в смысле нашего определения. Получится нечто гораздо более беспорядочное. Как мы увидим в дальнейшем, в реальном мире существуют сети, не относящиеся к безмасштабным и гораздо более хаотические, чем те, которые к этому разряду относятся.

Масштабно-инвариантный мир хаотичен по самой своей природе, так что ему определенно нет места в Тихонии. Как мы видели, масштабная инвариантность бывает свойственна не только сетям, но и облакам, снежинкам, кротовым ходам, папоротнику, готической архитектуре, финансовым рынкам и многим другим природным и социальным явлениям. По сравнению с Тихонией масштабно-инвариантный мир хаотичен, непредсказуем и экстремален, даже в самой «тихой» своей форме, а именно в ситуациях, в которых фактор Мандельброта близок к 0. В то же время самые «дикие» формы масштабной инвариантности, с фактором Мандельброта, равным 2 или даже больше того, представляют собой сравнительно тихие формы Диконии. По меньшей мере в них действует некий руководящий принцип — масштабная инвариантность.

Масштабно-инвариантному миру присуща своего рода умеренная или тихая дикость : в нем уже не действуют законы Тихонии, но и полноценная дикость Диконии до некоторой степени сдерживается организующим принципом. Более того, и в этом тихо-диком мире есть части более тихие и более дикие. В более тихих частях фактор Мандельброта меньше 1, в то время как у более диких, в которых этот фактор больше 1, даже нет стандартного отклонения. Если фактор Мандельброта α меньше 1, то, по мере того как мы исследуем связи некой вершины, потом — связи всех вершин, соединенных с первой, потом — связи каждой новой вершины и так далее, доля известных нам вершин растет и асимптотически приближается к 100 %. Чем меньше значение α, тем быстрее наше знание о сети приближается к стопроцентному.

Если α = 1, наше знание о данной вершине остается постоянным: доля неизвестных нам связей остается приблизительно неизменной, и число открытых новых вершин приблизительно равно числу вершин уже исследованных.

Если α > 1, то чем больше связей какой-либо вершины мы исследуем, тем больше становится доля еще не исследованных вершин. Доля известных нам соединений падает и асимптотически приближается к 0 %, потому что у вершины обнаруживаются все новые и новые связанные вершины, по большей части нам неизвестные, причем быстрее, чем мы успеваем их исследовать. Чем больше значение α, тем быстрее доля известного нам приближается к 0 %.