Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Первое простое число – 2. Мы поселим число 1 в номере 2, а число 2 – в номере 2², число 3 получит номер 2³, число 4 будет жить в номере 2 4… и так далее. Следующее простое число – 3, – продолжал профессор. – Поэтому дробь 1/2 поселится в номере 3, 2/2 – в номере 3², 3/2 – в номере 3³, 4/2 – в номере 3 4и так далее.

– Но ведь 2/2 равно 1, а число 1 уже живет в номере 1, – задумалась администратор гостиницы.

– В этом нет никакой проблемы, даже наоборот. Числу 1 достанется множество номеров, и оно выберет, в каком из них жить, – ответил профессор.

Теперь мы подходим к третьему простому числу, которое равно 5. Значит, числу 1/3 достанется номер 5. – Именно в этот момент администратор поняла, почему простые числа непременно нужно возводить в степени: дело в том, что номер 4 уже занят числом 2.

– 2/3 поселится в номере 5², – продолжал профессор, – дроби 3/3 будет выделен номер 5³… вы ведь уже поняли логику моего метода. Затем мы переходим к 7, четвертому простому числу. Идея остается той же. 1/4 получает номер 7, 2/4 – номер 7², 3/4 сможет вселиться в номер 7³ и так далее и так далее – снова и снова и снова. Эта схема расселения очень интересна, – добавил профессор. – Хотя имеется бесконечное число бесконечных групп постояльцев, и каждая из этих групп сама по себе способна целиком заполнить гостиницу, мы сумели разместить всех их. Причем… у нас по-прежнему остается бесконечное количество свободных номеров!

– Что?! – Администратор гостиницы не поверила своим ушам.

– Все номера, не соответствующие простым числам или степеням простых чисел, – например 1, 6, 10, 12, 14, 15, 18… – остаются совершенно пустыми.

Администратор, лишь мгновением раньше бывшая в восторге от того блестящего метода, который предложил для решения проблемы расселения профессор, снова впала в полнейшее отчаяние. Перед ней снова возникла проблема уровня заполненности гостиницы. Хороший администратор гостиницы просто не может позволить себе иметь бесконечно много (!) незанятых номеров. Что подумают хозяева гостиницы?

– Послушайте, – сказала Омега профессору, – одни только натуральные числа могут заполнить всю гостиницу, и так оно раньше и было. А теперь вы предлагаете какую-то безумную схему, по которой натуральные числа вместе с бесконечным количеством других бесконечных множеств, каждое из которых тоже могло бы заселить всю гостиницу, создают мне уровень заполненности гораздо ниже 100 процентов. По-моему, в этом нет никакой логики. Я, конечно, не специалист, но нет ли какого-нибудь способа, который позволил бы мне отчитаться начальству о значительно более высокой заполненности гостиницы?

– Что же, я думал, что решение будет гораздо более эффектным, если останется бесконечное число незанятых номеров. Но если вас интересует только уровень заполненности, я могу предложить другой вариант, в котором все номера будут заполнены на 100 процентов.

– Пожалуйста, расскажите мне о нем! – взмолилась Омега.

– Прежде чем я объясню это решение, нам нужно провести небольшую подготовку. Поставим в соответствие каждому рациональному числу пару чисел. Первым из них будет его числитель, а вторым – знаменатель. Например, числу 3/4 будет соответствовать пара чисел (3, 4). Каждое натуральное число n мы будем записывать в виде дроби n /1; тогда ему будет соответствовать пара ( n , 1). Например, числу 7 соответствует пара (7, 1). Теперь расположим все эти числа следующим образом:

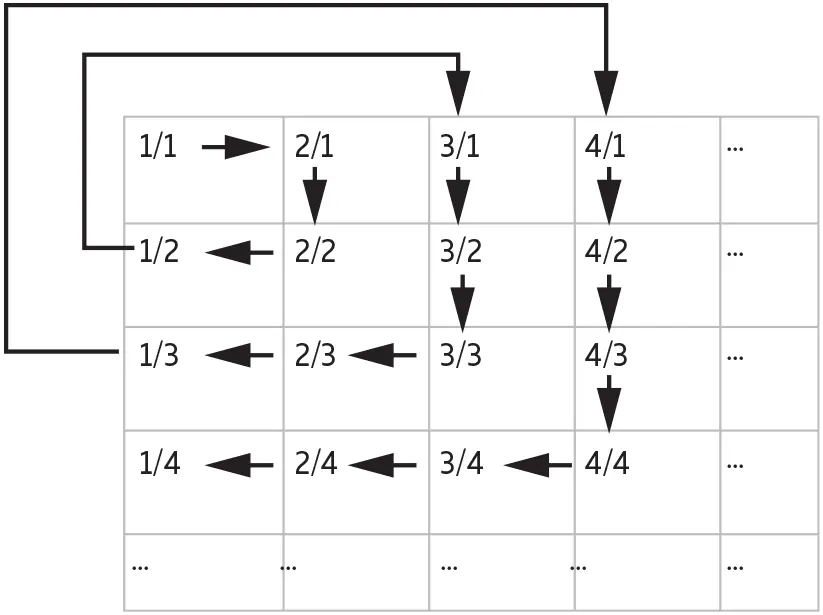
Отмечу для любителей алгебры, что в общем случае мы выделяем числу n / m номер n ² – m + 1, если n ≥ m , и номер ( m – 1)² + n , если n < m .

Например, у числа 3/2 числитель больше знаменателя; следовательно, ему должен быть предоставлен номер 3² – 2 + 1, то есть номер 8. Можете убедиться сами: если начать с пары (1, 1) и следовать по стрелкам (см. приведенный выше чертеж), то клетка с парой (3, 2) будет восьмой на этом пути.

Администратор была вне себя от счастья. Она даже запустила новую рекламную кампанию под лозунгом «Мы бесконечно рады всем!».

Профессор Финкельштейн-Островский-Канторович отметил, что существует огромное количество разных способов расселения в гостинице рациональных чисел:

– Вот один из этих способов. Определим для каждой дроби n / m «высоту», равную сумме числителя и знаменателя этой дроби. Другими словами, пусть высота h дроби n / m равна n + m . Наименьшая такая высота равна 2, причем есть только одна дробь с такой высотой – а именно 1/1. Есть два рациональных числа, высота которых равна 3; это числа 1/2 и 2/1. У чисел 1/3, 2/2 и 3/1 высота h = 4, а таких чисел, для которых h = 5, существует четыре: 1/4, 2/3, 2/3, 4/1. Таким образом, все рациональные числа можно расположить в порядке возрастания их высоты {28} 28 Числа с равной высотой располагаются в порядке возрастания числителя. .