Gustavo Pineiro - У интуиции есть своя логика. Гёдель. Теоремы о неполноте.

В 1890-м, за год до смерти Кронекера, Кантор был выбран председателем недавно созданного Немецкого математического общества, и его идея считать теорию множеств базой и основанием математики начинала набирать сторонников. Одним из них был немецкий логик Готлоб Фреге.

Готлоб Фреге родился в 1848 году, то есть он принадлежал к тому же поколению, что и Кантор. Фреге принял теорию множеств с самого начала и стал одним из защитников идеи о том, что эта теория должна стать базой для остальной математики.

Немецкое слово Begriffsschrift, которое Готлоб Фреге использовал для обозначения символической структуры, созданной им для логики и математики, обычно переводится как концептография, что дословно означает «рисунок концептов».

Как мы можем увидеть на изображении справа, символизм Фреге приближается скорее к линейному рисунку, чем к написанному тексту. Здесь показана теорема 71 из его книги «Исчисление понятий...», и ее перевод следующий: f — это процедура, a F — свойство, которое сохраняется при применении процедуры f. Если x обладает свойством, а y получен из х посредством применения процедуры f, то у также обладает этим свойством.

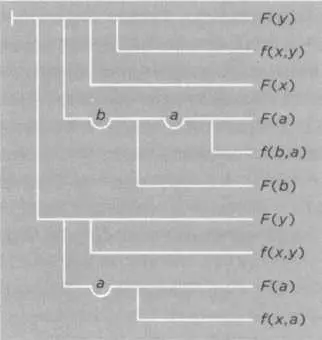
Хотя Фреге был согласен с Кантором в целом, у него было много формальных критических замечаний. По мнению Фреге, статьи Кантора были написаны недостаточно научным языком, без четкого разграничения аксиом (утверждений, которые принимаются без доказательств) и теорем (утверждений, которые доказываются на основе аксиом). Кантор все время взывал к интуиции читателя, что Фреге критиковал и называл психологизмом. Математика, по его мнению, должна пользоваться строгим языком со специально созданными символами. Все рассуждения должны быть выражены ясно, лишены двусмысленностей и взывания к интуиции. Фреге посвятил почти всю свою жизнь развитию этой идеи. В одной из своих основополагающих работ, «Исчисление понятий, или подражающий арифметике формальный язык чистого мышления» (1879), Фреге объясняет свой символический язык, очень отличающийся от нашего обычного письма (он похож скорее на линейный рисунок, чем на текст). Это вызывало сложности в понимании и у современников ученого, и даже сегодня. Возможно, Фреге намеренно хотел дистанцировать символическую запись от естественного языка, но стратегически это было ошибкой, поскольку затруднило понимание работы широкой аудиторией.

В 1893 году Фреге опубликовал первый том «Основных законов арифметики», первую часть работы всей своей жизни, в которой изложил строгое определение натуральных чисел на основе логики и теории множеств. Почти через десять лет, 16 июня 1902 года (за четыре года до рождения Гёделя), когда Фреге уже отправил в печать второй том «Основных законов...», он получил письмо от Бертрана Рассела, отправленное из Фрайдиз Хилл, Хаслмир (Великобритания). Письмо занимало одну страницу, однако этого было достаточно для того, чтобы развязать кризис оснований. Рассел начал с похвалы работы Фреге и выразил свою абсолютную поддержку автору. «Но я нашел небольшую сложность», — пишет Рассел.

Этой небольшой сложностью была одна из аксиом, на которых Фреге основывал теорию множеств, — так называемая аксиома выделения. В ней говорится, что каждому свойству назначается множество (множество объектов, которые обладают этим свойством). Например, свойству «быть четным числом» соответствует множество, образованное всеми четными числами; свойству «быть планетой Солнечной системы» соответствует множество всех планет Солнечной системы, и так далее. На первый взгляд эта аксиома кажется абсолютно невинным утверждением, неспособным породить какую-либо проблему. Однако Рассел задал свойство «быть множеством, которое не является членом самого себя».

Поразмышляем об этой идее.

Множества образованы членами (также существует пустое множество, не имеющее членов, но мы можем оставить его за рамками нашего анализа). Например, множество планет Солнечной системы состоит из (насколько мы знаем) восьми членов: Меркурия, Венеры, Земли, Марса, Юпитера, Сатурна, Урана и Нептуна. Объект «множество планет Солнечной системы» — это абстрактная сущность, существующая только как идея и собирающая под одним названием восемь планет. Каждый из членов этого множества — наоборот, конкретная планета, а не абстракция. Множество планет Солнечной системы не входит в список самих членов: оно не является членом самого себя. Рассел выражал эту идею следующим образом: «Множество, образованное лошадьми, — не лошадь» (мы можем сесть на лошадь, но не на абстрактную сущность). Но некоторые множества действительно являются членами самих себя. Например, подумаем о множестве всех абстрактных сущностей. Оно само является абстрактной сущностью и, следовательно, членом самого себя.