Gustavo Pineiro - У интуиции есть своя логика. Гёдель. Теоремы о неполноте.

"Направление знаний устремляется к немеханической реальности: Вселенная теперь больше похожа на великую мысль, чем на великую машину. Разум уже не кажется неким существом, случайно вторгшимся в королевство материи... мы скорее должны приветствовать его как создателя и властелина королевства материи".

Джеймс Джинс скончался в графстве Суррей (Англия) в 1946 году.

Последняя научная работа по математической логике за авторством Гёделя появилась в форме книги объемом примерно 70 страниц, опубликованной издательством Принстонского университета в 1940 году. Она не была напрямую написана Гёделем, а представляла собой издание конспектов курса, прочитанного ученым в 1938-1939 годах в Институте перспективных исследований. Книга называется "Совместимость аксиомы выбора и обобщенной континуум-гипотезы с аксиомами теории множеств", и в ней изложено частичное решение первой из проблем, которые поставил Давид Гильберт на своей знаменитой лекции 1900 года, — проблемы, изначально сформулированной Георгом Кантором и известной как континуум-гипотеза.

Чтобы понять, что такое континуум-гипотеза, мы должны вернуться к теории Кантора о бесконечности, о которой говорилось в первой главе. Вспомним, что множество, по словам самого Кантора, это "собрания целиком объектов действительности или нашей мысли". Так, имеется множество всех дней недели, множество всех месяцев в году или множество четных натуральных чисел. Одни из этих множеств конечны, другие бесконечны.

Множество является конечным, когда возможно сосчитать его члены один за другим, и этот счет в какой-то момент заканчивается. В бесконечных множествах, наоборот, счет никогда не заканчивается. Если у нас есть конечное множество, мы вполне можем сказать, сколько в нем членов; например, во множестве дней недели семь членов, а во множестве месяцев года — 12. Количество членов множества математики называют его кардинальным числом; таким образом, мы можем сказать, что кардинальное число множества, образованного буквами слова "море", равно четырем.

Целью Кантора было придать смысл идее кардинального числа, или количества членов, для бесконечных множеств. Но как можно говорить о количестве членов бесконечного множества? Можно ли что-то сказать, кроме очевидного факта того, что оно бесконечно? Кантор исходил из простой идеи: представим себе, что в большом зале много играющих детей и большое число стульев (рисунок 1), и нам хочется знать, равно ли их количество друг другу. Один из способов сделать это — это сосчитать детей по одному, сделать то же самое со стульями, а затем сравнить результаты.

РИС. 1

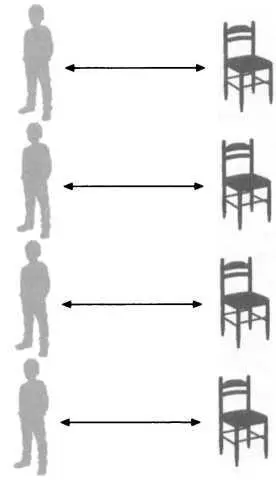
РИС. 2

Но есть более прямой способ осуществить это сравнение — попросить детей сесть по одному на каждый стул. Если не осталось ни одного пустого стула, мы можем сказать, что стульев ровно столько же, сколько и детей, то есть что кардинальные числа множества стульев и множества детей равны. В математической терминологии можно сказать, что мы установили биективное (взаимнооднозначное) соответствие между множествами (каждому ребенку соответствует один стул, а каждому стулу — один ребенок).

Итак, мы можем сказать, что у двух конечных множеств одно и то же кардинальное число, если можно установить биективное соответствие между ними. Идея Кантора заключалась в том, чтобы распространить это понятие на бесконечные множества, установив биективное соответствие между множествами в виде сравнения их кардинальных чисел.

На основе этой идеи Кантор определил, что два бесконечных множества имеют одно и то же кардинальное число, если можно установить между ними биективное соответствие, то есть если можно установить пары между их соответствующими членами так, чтобы каждому члену первого множества точно соответствовал один член второго, и наоборот.

В первой главе мы уже видели, что множество всех натуральных чисел (1, 2, 3, 4,...) может иметь биективное соответствие с множеством квадратных чисел (1,4, 9, 16,...).

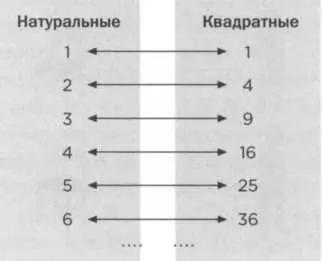
Множество натуральных чисел обычно обозначают буквой N (буква символизирует числа в целом как самостоятельный объект). А если к натуральным числам добавить их противоположные (то есть отрицательные числа -1, -2, -3, -4, ...), а также ноль, мы получим множество целых чисел, которое в математике обычно обозначается буквой Z — от первой буквы немецкого слова Zahl (число).