Яков Перельман - Живой учебник геометрии

Р е ш е н и е. Около точки С, как около центра, описываем каким-нибудь радиусом дугу АВ (черт. 144);

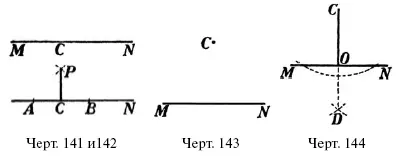
затем около точек А и В каким-нибудь радиусом описываем дуги D . Прямая DС перпендикулярна к МN . Чтобы убедиться в этом, соединим С и D с А и В .

Треугольники ACD и ВCD равны ( ССС ), следовательно, уг. ACD = уг. DCВ , и значит, треугольник АСО = ВСО ( СУС ). Отсюда уг. AОС = уг. ВОС , а так как эти углы смежные, то они прямые.

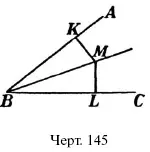
56. Объясните, почему каждая точка М прямой ВM , делящей пополам угол АВС (черт. 145) одинаково отстоит от сторон АВ и ВС угла (т. е. почему, например, MK = ML ?).

Р е ш е н и е. Треугольники ВML и ВМК равны ( УСУ ).

Треугольник с тремя равными сторонами называется р а в н о с т о р о н н и м. Так как против равных сторон в одном и том же треугольнике лежат равные углы, то все углы равностороннего треугольника равны, и, следовательно, каждый из них равен. 180°: 3 = 60°.

Обратно: если каждый угол треугольника равен 60°, то все стороны такого треугольника одинаковы, – потому что, против равных углов в одном и том же треугольнике лежат, равные стороны.

Применения

57. Без транспортира построить угол в 60°. В 30°. В 15°. В 120°. В 75°.

Р е ш е н и е. Строим равносторонний треугольник произвольных размеров; каждый его угол = 60°. Разделив угол этого треугольника пополам, получим угол в 30°. Разделив еще раз пополам, будем иметь угол в 15°. Угол в 120° = 90° + 30°. Угол в 75° =60° + 15° = 90° – 15°.

Предварительное упражнение

Равносторонний треугольник разбит равноделящей одного из углов на два треугольника. Определить их углы.

уг. D = 60°; а так как и уг. ABD = 60°, то треугольник ABD – равносторонний, и следовательно, AD = АВ . Но АС = 1/2 АD (почему?); отсюда АС = 1/2 АВ .

Итак, мы убедились, что

к а т е т п р о т и в у г л а в 30° р а в е н п о л о в и н е г и п о т е н у з ы.

Применения

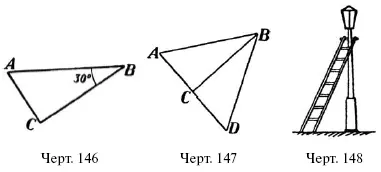
58. Лестница длиною 6 м приставлена к фонарному столбу под углом 30° к нему (черт 148). Каково расстояние от основания лестницы до основания фонаря?

Р е ш е н и е. Так как катет против 30° равен половине гипотенузы, то искомое расстояние = 3 м.

59. Длина стропильной ноги АС (черт. 137) вдвое больше высоты AD стропильной фермы. Определить угол наклона этой кровли к горизонту.

Р е ш е н и е. Искомый угол СAD = 30°, так как только при таком условии CD равно половине АС .

Пусть у нас имеется прямоугольный треугольник (черт. 146) ABC , один угол которого, именно В , равен 30°. Перегнем мысленно треугольник по катету ВС . Тогда займет положение ВСD (черт. 147), при чем CD составит продолжение АС , потому что уг. ВСD + ВСА = развернутому. Уг. СВD = уг. ABC = 30°; значит, уг. А = 60°;

Мы знаем, что если в треугольнике есть равные стороны, то углы, лежащие против них, тоже равны. Рассмотрим теперь, каково соотношение между сторонами и углами в случае н е р а в н ы х сторон.

Предварительное упражнение

В фигуре черт. 149 укажите какой угол больше: уг. 1 или у г. 2?

В фигуре черт. 151 АВ = AD . Какой угол больше; уг. С или у г. 1?

Покажем, что в

т р е у г о л ь н и к е с н е р а в н ы м и с т о р о н а м и п р о т и в б о л ь ш е й с т о р о н ы л е ж и т б о л ь ш и й у г о л. Пусть в треугольнике АВС (черт. 150) сторона АС больше «стороны АВ . Отложим от вершины образуемого ими угла меньшую сторону АВ на большей АС получим точку D . Соединив D с В , имеем равнобедренный треугольник ABD , в котором угол 1 = уг. 2. Угол С меньше угла 1, а значить, подавно меньше угла. ABC . Таким образом мы убеждаемся, что против большей стороны [АС] лежит больший угол [ABC] .

Нетрудно удостовериться, что и обратно: если в треугольнике имеются неравные углы, то

п р о т и в б о л ь ш е г о у г л а л е ж и т б о л ь ш а я с т о р о н а.

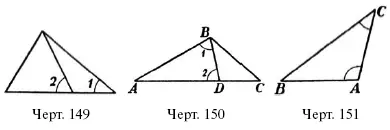
Пусть мы знаем, что в треугольнике (черт. 151) ABC уг. А больше угла С . Тогда сторона ВС не может быть равна АВ : иначе уг. А равнялся бы углу С ; не может сторона ВС быть и м е н ь ш е: АВ – тогда уг. А был бы м е н ь ш е угла С (а мы знаем, что уг. А б о л ь ш е уг. С ). Не равен и не меньше, значит – больше.