Яков Перельман - Живой учебник геометрии

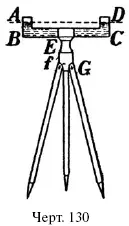
Способ этот очень хлопотлив и применим только для небольших расстояний. Нивелирование на большом расстоянии выполняют иначе, – именно при. помощи особого прибора, называемого нивелиром (черт. 130). Устройство прибора несложно: две отвесные трубки, сообщающиеся посредством соединительной трубки, установлены на треноге. В трубки налита вода; так как она в обоих сосудах стоит на одинаковом уровне, то прямая AD, проходящая через оба уровня, должна быть горизонтальна.

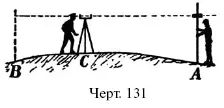
Разность высот точек А и В (черт. 131) определяют помощью нивелира так. Помещают нивелир в промежуточную точку С , а в точку А ставят отвесно рейку, разделенную на дециметры и сантиметры (черт. 132). Вдоль рейки ходит дощечка, которую подвигают до тех пор, пока ее средняя линия не будет видна наблюдателю у нивеллира на одной линии с обоими уровнями воды в сосудах. Заметив положение дощечки, переносят рейку в точку В, не изменяя положения нивеллира. Дощечку снова помещают на одной высоте с уровнями воды в сосудах. Разность высот дощечки покажет, насколько разнятся высоты точек А и В.

Если требуется определить высоту целого ряда точек местности (В, С, D на черт. 133) над или под горизонтальной плоскостью, проходящей через А , то поступают следующим образом. Поместив нивелир между А и В , находят высоту А над В , как сейчас было объяснено. Затем, перенеся нивелир между В и С , находят высоту В над С . Сложив обе разницы в высотах, находим возвышение А над С . Подвигаясь таким образом дальше, мы доходим до точки Е , которая выше предыдущей точки D . Ясно, что тогда надо будет ее соответственно уменьшить разность высот А и D чтобы узнать возвышение точки А над Е . Таким путем к концу работы определятся разности высот для всех точек нивелируемого «профиля» ABCDEF .

Короче говоря, надо сложить отдельно все показания при взглядах вперед и все показания при взглядах назад, и из первой суммы вычесть вторую. В результате получим возвышение конечной точки над начальной; отрицательный результат покажет, насколько конечная точка ниже начальной.

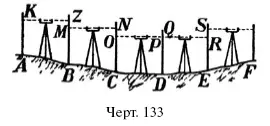
Разность высот конечных точек А и F можно найти и не производя вычислений для каждой промежуточной точки. Обозначим положение дощечки на рейке в точке А через а ; в точке В – через b при взгляде вперед и через b 1, при взгляде назад; в точке С – через с и с 1, в точке D – через d и d 1 и т. д. Чтобы найти разность высот А и F мы произвели следующие действия:

[ b – а ] + [ с – b 1] + ( d – с 1) – ( е – d 1) – [ е 1 – f ].

Раскрыв скобки, имеем

b – а + с – b 1 + d – с 1 – е – d 1 – е 1 – f

или

b + с + d + е + f – [ а + b 1 + с 1 + d 1 + е 1].

С основными свойствами всякого треугольника мы познакомились в §§ 15–22. Самые главные из них следующие: сумма углов треугольника равна 180°; треугольники равны друг другу или по трем сторонам, или по двум сторонам и углу между ними, или по одной стороне и двум углам (для краткости мы обозначили эти случаи так: ССС, СУС, УСУ ). Теперь познакомимся с некоторыми новыми свойствами треугольников.

Предварительные упражнения

Укажите равные треугольники в фигуре черт. 134, где АВ = АС , a AD – равноделящая угла А .

Каковы углы ADB и ADС на черт. 134: острые или тупые?

Мы знаем, что в р а в н ы х треугольниках против равных сторон лежат равные углы. Покажем, что и

в о д н о м и т о м ж е т р е у г о л ь н и к е п р о т и в р а в н ы х с т о р о н л е ж а т р а в н ы е у г л ы.

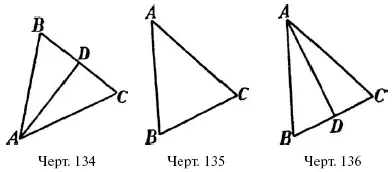
Пусть у нас взят треугольник ABC (черт. 135), в котором сторона АВ равна стороне АС . Легко убедиться, что в таком треугольнике углы В и С , лежащие против равных сторон, равны между собой. Если в нашем треугольнике проведем (черт. 136) равноделящую АD угла А , она разобьет ABC на два треугольника: АDB и АDС , которые равны между собой ( СУС ). По этому угол В , лежащий против AD , равен углу С , лежащему против той же общей стороны.