Яков Перельман - Живой учебник геометрии

Применения

28. На прямоугольное поле шириною 135 м и длиною 240 м выпало дождевой воды 3 мм. Сколько куб. метров воды выпало на все поле?

Р е ш е н и е. Искомый объем равен

135 ? 240 ? 0,003 = 100 куб. м.

29. Прямоугольный бак в 1 м ширины и 140 см длины налит водою. Когда под воду окунулся человек, уровень воды поднялся на 4 см. Как велик объем тела этого человека?

Р е ш е н и е. Объем тела человека равен 100 ? 140 ? 4 = 60 000 куб. см.

30. Если куб с ребром 1 см представить себе разделенным на кубики с ребром в 0,1 мм, то во сколько раз общая поверхность всех этих мелких кубиков будет больше поверхности первоначального куба?

Р е ш е н и е. Поверхность куба с ребром 1 см равна 6 кв. см = 600 кв. мм. Поверхность кубика с ребром 0,1 мм равна 6 0,01 = 0,06 кв. мм. Число этих кубиков равно 100 ? 100 ? 100 = 1 000 000. Общая поверхность кубиков будет 0,06 ? 1 000 000 = 60 000 кв. мм, т. е. общая поверхность увеличится в 100 раз.

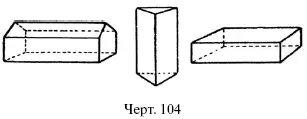
П р я м о ю п р и з м о ю называется тело, две грани (о с н о в а н и я) которого представляют собою треугольники, четырехугольники или многоугольники, а все остальные (б о к о в ы е) – прямоугольники (черт. 104). Рассмотренный раньше прямоугольный параллелепипед можно отнести к призмам: это прямая призма с прямоугольными основаниями. Если основания прямой призмы треугольники, то призма «треугольная», если квадрат, то призма «квадратная»; если вообще четырехугольники, то «четырехугольная»; если какие-нибудь многоугольники, то «многоугольная», напр. «восьмиугольная», и т. п.

Объем прямоугольной призмы, т. е. прямоугольного параллелепипеда, мы уже умеем вычислять: для этого нужно умножить ее длину на ширину и на высоту. Так как произведение длины ^прямоугольника на его ширину дает его площадь, то предыдущее – правило мы можем высказать иначе, а именно так:

о б ъ е м п р я м о у г о л ь н о й п р и з м ы

р а в е н п р о и з в е д е н и ю п л о щ а д и е е о с н о в а н и я н а в ы с о т у. Если площадь основания такой призмы обозначить через s, а высоту – через h , то объем ее V = sh .

Можно убедиться, что та же формула применима и ко всякой прямой призме, какую бы форму ни имело ее основание. Действительно, на каждый квадратный сантиметр основания прямой призмы опирается столб, высота которого равна высоте призмы ( h ). Все эти столбы, вместе взятые, составляют объем призмы. Но объем каждого столба равен 1 кв. см Ч h см = h куб. см; число же столбов равно числу кв. см, заключающихся в основании призмы. Если площадь основания 5 кв. см, то число призм будет s, а сумма их объемов s ? h = sh куб. см. Это и будет объем призмы.

Итак,

О б ъ е м в с я к о й п р я м о й п р и з м ы р а в е н п р о и з в е д е н и ю п л о щ а д и е е о с н о в а н и я н а в ы с о т у.

Повторительные вопросы

Что называется прямой призмой? – Что такое прямая прямоугольная призма? Квадратная? Треугольная? Шестиугольная? – Как вычисляется объем всякой прямой призмы? – Выразите это правило формулой.

Применения

31. Вычислить объем прямой т р е у г о л ь н о й призмы, если ее высота 16 см, а треугольник, лежащий в основании призмы, имеет основание 7 см и высоту – 5 см.

Р е ш е н и е. Вычисление объема начнем с определения площади основания; она равна 0,5 7 5 = 18 кв. см. Умножив основание призмы на высоту, 18 16, узнаем ее объем – 290 куб. см.

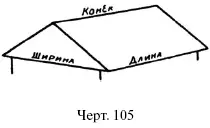
32. Чердачное помещение (черт. 105) имеет форму прямой треугольной призмы. Длина его – 14 м, ширина – 8,1 м, а высота конька – 3,2 метра. Найти объем («кубатуру») этого помещения.

Р е ш е н и е. Кубатура равна 1/2 ? 8,1 ? 3,2 ? 14 = 180 куб. м.

33. Какова площадь основания прямой многогранной призмы, объем которой 720 куб. см, а высота 18 см?

Р е ш е н и е. Основание определится, если разделить объем (720) на высоту (18). Получим 40 см.

В метрической системе мер единицей веса служит вес одного кубического сантиметра чистой воды – грамм (г).

Тысяча граммов составляют килограмм (кг), а тысяча килограммов – тонну (т). Нетрудно сообразить, какой объем занимают эти количества воды. 1 грамм воды занимает, конечно, 1 куб. см. Килограмм воды занимает объем в 1000 раз больший, т. е. 1000 куб. см = 1 куб. дециметру; значит, килограмм есть вес 1 куб. дециметра воды. Далее, тонна воды занимает объем в 1000 раз больший, чем килограмм, т. е. 1000 куб дм; но 1000 куб. дм = = 1 куб. метру; значит, тонна есть вес 1 куб. метра воды. Запомним эти соотношения: