Яков Перельман - Живой учебник геометрии

1 куб. см воды весит 1 грамм

1 куб. дм»» 1 килограмм

1 куб. м»» 1 тонну.

Зная это, можно по объему воды вычислить ее вес (без взвешивания), и наоборот, по весу воды найти (без измерения) ее объем. Покажем на нескольких примерах, как это делается.

34. В прямоугольный аквариум, ширина которого 20 см, а длина 35 см, налито воды до высоты 12 см. Сколько весит вода в аквариуме?

Р е ш е н и е. Находим сначала объем воды в аквариуме; он равен 20 ? 35 ? 12, т. е. 8 400 куб. см. Так как каждый куб. см воды весит 1 грамм, то вода в аквариуме весит 8400 граммов, или 8,4 кг.

35. Сколько весит вода в прямоугольном баке длиною 1,5 м и шириною 1 м, если она налита до высоты 0,6 м?

Р е ш е н и е. Объем воды в баке равен 1,5 ? 1 ? 0,6 = 0,9 куб. м. Так как 1 куб. метр воды весит 1 тонну, то вода в баке весит 0,9 тонны.

Подобным же образом можно по объему вычислять вес тел и из любого другого материала, если знать, сколько весит 1 куб. сантиметр этого материала. Очень полезно поэтому располагать таблицей, в которой указано, сколько весит 1 куб. сантиметр различных веществ.

Вес 1 куб. сантиметра вещества называются удельным весом этого вещества. Краткая табличка удельных весов наиболее употребительных материалов здесь приведена.

Таблица удельных весов

Твердые тела

Золото. . . . . . . . . . . . . 19,3 грамма

Свинец. . . . . . . . . . . . 11,4»

Серебро. . . . . . . . . . . . 10,5»

Медь кованая. . . . . . . . . . 8,9»

Латунь. . . . . . . . . . . . . 8,5»

Железо, сталь, чугун. . . . . . . 7,8»

Олово. . . . . . . . . . . . . 7,3»

Цинк. . . . . . . . . . . . . 7,1»

Алюминий. . . . . . . . . . . 2,6»

Гранит. . . . . . . . . . . . . 2,5»

Стекло оконное. . . . . . . . . 2,5»

Лед. . . . . . . . . . . . . . 0,9»

Дерево сосновое сухое. . . . . . 0,5»

Пробка. . . . . . . . . . . . 0,20»

Жидкости

Ртуть. . . . . . . . . . . . . 13,6 грамма

Вода чистая. . . . . . . . . . 1»

Спирт (100) керосин. . . . . . . 0,8»

Нефть. . . . . . . . . . . . . 0,76»

Числа этой таблицы показывают:

1) сколько граммов весит 1 куб. см данного вещества;

2) сколько килограммов весит 1 куб. дециметр этого вещества;

3) сколько тонн весит 1 куб. метр этого вещества.

Действительно, если 1 куб. см, например, алюминия весит 2,6 грамма, то 1 куб. дм должен весить в 1000 раз больше, т. е. такое же число килограммов, а 1 куб. метр еще в 1000 раз больше, т. е. такое же число тонн.

Из следующих примеров видно, как надо пользоваться этой таблицей для разных расчетов.

36. Сколько весит железный брусок длиною 0,6 м, шириною 2,5 см и толщиною 1,5 см?

Р е ш е н и е. Объем бруска в куб. см равен 60 ? 2,5 ? 1,5 = 225. В таблице находим, что 1 куб. см железа весит 7,8 г; следовательно, брусок весит 7,8 ? 225 = 1800 г = 1,8 кг.

37. Какой объем занимает полкилограмма свинца?

Р е ш е н и е. Каждые 11,4 грамма свинца занимают объем в 1 куб. см (см. таблицу). Значит, наш кусок свинца имеет в объеме столько куб. см, сколько раз в его весе заключается 11,4 г. Разделив 0,5 кг на 11,4 г получаем 500: 11,4 = 44.

Итак, объем 0,5 кг свинца – 44 куб. см.

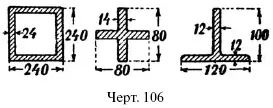
38. Найти вес 1 м железа, раз меры поперечного сечения которого указаны в мм на черт. 106.

Р е ш е н и е – по образцу предыдущих задач.

Повторительные вопросы

Какие вам известны единицы веса? – Что такое грамм? Килограмм? Тонна? – Какой объем занимает грамм воды? Килограмм воды? – Что такое удельный вес? – Что означают числа в таблице удельных весов?

Предварительное упражнение

Обтяните ниткой какой-нибудь круглый предмет (стакан, кастрюлю, решето) по окружности и, вытянув нитку, измерьте ее. Определите затем, во сколько раз длина окружности этого предмета больше ее диаметра.

На практике часто нужно бывает определять длину окружности. Чтобы заготовить, например, железную полосу для шины колеса, кузнецу нужно заранее знать длину этой полосы, т. е. длину окружности колеса. Всего проще в этом случае обтянуть обод колеса ниткой и затем, вытянув, измерить ее длину. Не всегда, однако, бывает удобно поступать так, а часто способ этот и вовсе неприменим: нельзя, например, найти по этому способу длину окружности, начерченной на бумаге.