Яков Перельман - Живой учебник геометрии

Рассуждение это нельзя прямо применить к треугольнику с тупым углом (черт. 92), потому что перпендикуляр CD встречает не основание АВ , а его продолжение. В этом случае приходится рассуждать иначе. Обозначим отрезок AD через p, BD – через, q , так что основание а треугольника равна p – q . Площадь нашего треугольника АВС равна р а з н о с т и площадей двух треугольников ADC – BDC = 1/2 ph – 1/2 qh = 1/2 h ( p – q ) = 1/2 ah .

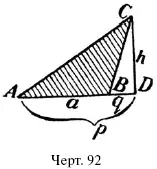
Итак, во всех случаях площадь треугольника равна половине произведения любого его основания на соответствующую высоту.

Отсюда следует, что треугольники с равными основаниями и высотами имеют одинаковые площади, или, как говорят,

р а в н о в е л и к и.

Равновеликими вообще называются фигуры, имеющие равные площади, хотя бы сами фигуры не были равны (т. е. не совпадали при наложении).

Повторительные вопросы

Что называется высотою треугольника? Основанием треугольника? – Сколько высот можно провести в одном треугольнике? – Начертите треугольник с тупым углом и проведите в нем все высоты. – Как вычисляется площадь треугольника? Как выразить это правило формулой? – Какие фигуры называются равновеликими?

Применения

22. Огород имеет форму треугольника с основанием 13,4 м и высокою 37,2 м… Сколько (по весу) требуется семян, чтобы засадить его капустой, если на кв. м идет 0,5 грамма семян?

Р е ш е н и е. Площадь огорода равна 13,4 ? 37,2 = 498 кв. м.

Семян потребуется 250 г.

23. Параллелограмм разбивается диагоналями на 4 треугольные части. Какая из них имеет наибольшую площадь?

Р е ш е н и е. Все 4 треугольника равновелики, так как имеют равные основания и высоты.

Правило вычисления площади параллелограмма устанавливается весьма просто, если разбить его диагональю на два треугольника. Например, площадь параллелограмма ABCD (черт. 93) равна удвоенной пощади каждого из двух равных треугольников, на которые он разбивается диагональю АС. Обозначив основание треугольника ADC через а , а высоту через h , получаем площадь S параллелограмма

S = ah.

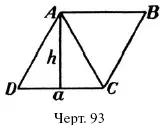
Перпендикуляр h называется «высотою параллелограмма», а сторона а, к которой он проведен, – «основанием параллелограмма». Поэтому установленное сейчас правило можно высказать так:

П л о щ а д ь п а р а л л е л о г р а м м а р а в н а п р о и з в е д е н и ю л ю б о г о е г о о с н о в а н и я н а с о о т в е т с т в у ю щ у ю в ы с о т у.

Повторительные вопросы

Что называется основанием и высотою параллелограмма? Как вычисляется площадь параллелограмма? – Выразите это правило формулой. – Во сколько раз площадь параллелограмма больше площади треугольника, имеющего одинаковые с ним основание и высоту? – При равных высотах и основаниях какая фигура имеет большую площадь: прямоугольник или параллелограмм?

Применение

24. Квадрат со стороною 12,4 см равновелик параллелограмму с высотою 8,8 см. Найти основание параллелограмма.

Р е ш е н и е. Площадь этого квадрата, а следовательно и параллелограмма равна 12,42= 154 кв. см. Искомое основание равно 154: 8,8 = 18 см.

Кроме параллелограммов, рассмотрим еще один вид четырехугольников – именно те, которые имеют только о д н у пару параллельных сторон (черт. 94). Такие фигуры называются т р а п е ц и я м и. Параллельные стороны трапеции называются ее о с н о в а н и я м и, а непараллельные – б о к а м и.

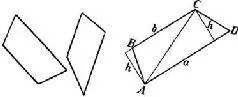
Черт. 94 Черт. 95

Установим правило вычисления плошали трапеции. Пусть требуется вычислить плошать трапеции ABCD (черт. 95), длина оснований которой a и b . Проведем диагональ АС, которая разрезает трапецию на два треугольника ACD и ABC . Мы знаем, что

площ. ACD = 1/2 ah

площ. ABC = 1/2 bh .

Значит:

площ. ABCD = 1/2 ah + 1/2 bh = 1/2 ( a + b ) h .

Так как расстояние h между основаниями трапеции называется ее высотою, то правило вычисления площади трапеции можно высказать так:

П л о щ а д ь т р а п е ц и и р а в н а п о л у с у м м е о с н о в а н и й, у м н о ж е н н о й н а в ы с о т у.