Яков Перельман - Живой учебник геометрии

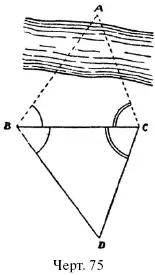
Р е ш е н и е. Треугольники ABC и ВDС равны по одной стороне ( ВС ) и двум углам (уг. DCB = уг. АСВ ; уг. DBC = уг. ABC .) Следовательно, АВ = ВD, как стороны, лежащие в равных треугольниках против равных углов.

От треугольников перейдем к четырехугольникам, т. е. к фигурам, ограниченным 4-мя сторонами. Примером четырехугольника может служить к в а д р а т – такой четырехугольник, все стороны которого равны, а все углы-прямые (черт. 76). Другой вид четырехугольника, тоже часто встречающийся, – п р я м о у г о л ь н и к:

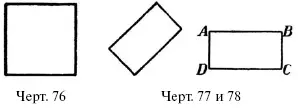
так называется всякий четырехугольник с 4-мя прямыми углами (черт. 77 и 78). Квадрат – тоже прямоугольник, но с равными сторонами.

Особенность прямоугольника (и квадрата) та, что обе пары его противоположных сторон п а р а л л е л ь н ы. В прямоугольнике ABCD, например (черт. 78), АВ параллельно DC , a AD параллельно ВС. Это следует из того, что обе противолежащие стороны перпендикулярны к одной и той же прямой, а мы знаем, что два перпендикуляра к одной прямой параллельны между собою (§ 16).

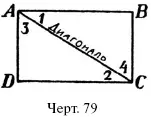
Другое свойство каждого прямоугольника то, что противоположные его стороны равны между собою. В этом можно убедиться, если соединить противоположные вершины прямоугольника прямой линией, т. е. провести в нем диагональ. Соединив А с С (черт. 79) мы получим два треугольника АВС и ADC. Легко показать, что эти треугольники равны друг другу: сторона АС – общая, уг. 1 = уг. 2, потому что это перекрестные углы при параллельных АВ и CD по такой же причине равны углы 3 и 4. По стороне же и двум углам треугольники ABC и ACD равны; следовательно, сторона АВ = стороне DС, и сторона AD = стороне ВС.

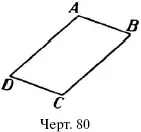
Такие четыреугольники, у которых, как у прямоугольников, противоположные стороны п а р а л л е л ь н ы, называются параллело граммами. На черт. 80 изображен пример параллелограмма: АВ параллельно DС, а AD параллельно BС. Черт.80

Прямоугольник – один из параллелограммов, а именно такой, у которого все углы прямые. Легко убедиться, что каждый параллелограмм обладает следующими свойствами:

П р о т и в о п о л о ж н ы е у г л ы п а р а л л ел о г р а м м а р а в н ы; п р о т и в о п о л о ж н ы е с т о р о н ы

п а р а л л е л о г р а м м а р а в н ы.

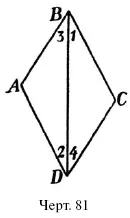
Чтобы убедиться в этом, проведем в параллелограмме ABCD (черт. 81) прямую ВD (диагональ) и сравним треугольники ABD и ВDC. Эти треугольники равны (случай УСУ ): BD – общая сторона; уг. 1 = уг. 2, уг. 3 = уг. 4 (почему?). Отсюда вытекают перечисленные раньше свойства.

Параллелограмм с четырьмя равными сторонами называется р о м б о м.

Повторительные вопросы

Какая фигура называется квадратом? Прямоугольником? – Что называется диагональю? – Какая фигура называется параллелограммом? Ромбом? – Укажите свойства углов и сторон всякого параллелограмма. – Какой прямоугольник называется квадратом? – Какой параллелограмм называется прямоугольником? – В чем сходство и различие между квадратом и ромбом.

Применения

15. Квадрат чертят так: отложив одну сторону проводят к ней на концах перпендикуляры, откладывают на них такие же длины и соединяют концы прямой линией (черт. 82). Как убедиться, что четвертая сторона, начерченного четырехугольника равна трем остальным и что все углы его прямые?

Р е ш е н и е. Если построение велось так, что к стороне АВ в точках А и В были проведены перпендикуляры, на которых отложены: АС = АВ и DВ = AB , то остается доказать, что углы С и D прямые и что CD равно АВ. Для этого проведем (черт. 83) диагональ AD. Уг. CAD = ADB, как соответственные (при каких параллельных?); АС = DB , а потому треугольники CAD и BAD равны (по признаку СУС). Отсюда выводим, что CD = AB и уг. С = прямому углу В . Как доказать, что четвертый угол CDB тоже прямой?