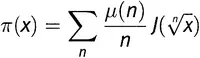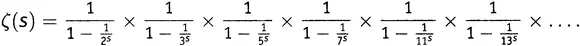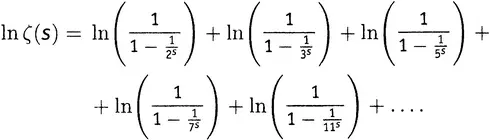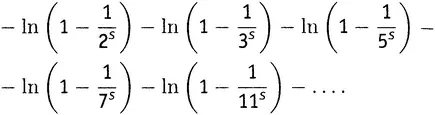Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Для полноты представления функции J на рисунке 19.3 изображен график J(x) при аргументах до 100. Самый маленький прыжок здесь совершается при x = 64 — это число представляет собой шестую степень (64 = 2 6), так что функция J прыгает при x = 64 на одну шестую.

Рисунок 19.3.Еще о функции J(x).

Какую пользу может принести подобная функция? Терпение, терпение. Сначала придется совершить один из тех логических скачков, о которых я предупреждал в начале главы.

Напоминаю в который уже раз, что у математиков есть масса способов обращать соотношения. Дали нам выражение для P через Q — отлично, посмотрим, не найдется ли способа выразить Q через P . В течение столетий в математике был развит целый инструментарий для того, чтобы совершать обращения, — он включает набор приемов для использования в самых разных условиях и обстоятельствах. Один из таких приемов носит название мебиусова обращения, и оно-то нам сейчас и нужно.

Не буду пытаться объяснить мебиусово обращение в общем виде. Оно описано в любом хорошем учебнике по теории чисел (см., например, раздел 16.4 в классической монографии «Теория чисел» Харди и Райта), а кроме того, поиск в Интернете наведет вас на множество ссылок. Подражая до некоторой степени самим функциям π и J , я вместо того, чтобы уныло тащиться от одной точки в моих рассуждениях к другой, перескочу сразу к следующему факту: применение мебиусова обращения к выражению (19.1)дает такой результат:

Можно заметить, что некоторые члены (четвертый, восьмой, девятый) здесь отсутствуют. А из тех, что присутствуют, некоторые (первый, шестой, десятый) входят со знаком плюс, тогда как другие (второй, третий, пятый, седьмой) — со знаком минус. Ничего не напоминает? Здесь спрятана функция Мебиуса из главы 15. На самом деле

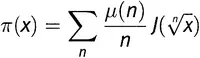
(где 1√x как и в других местах в книге, есть, конечно, просто x ). Почему, как вам теперь кажется, это назвали мебиусовым обращением?

Итак, мы записали функцию π(x) , выразив ее через J(x) . Это чудесно, потому что Риман нашел способ, как выразить J(x) через ζ(x).

Прежде чем расстаться с выражением (19.2), надо еще упомянуть, что, подобно выражению (19.1), это не бесконечная сумма, а конечная. Это происходит из-за того, что функция J , как и функция π , равна нулю, когда x меньше 2 (взгляните на график!), а если последовательно извлекать корни из какого-нибудь числа, то результат рано или поздно упадет ниже 2 и там останется. Например,

что дает в точности число 25, которое и в самом деле является числом простых чисел меньших 100. Волшебство.

А теперь повернем Золотой Ключ.

Вот Золотой Ключ, первое равенство в статье Римана 1859 года, полученное нами в главе 7, когда я убеждал вас, что это просто хитрый способ переписать решето Эратосфена:

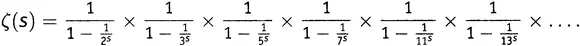
He будем забывать, что числа, появляющиеся в правой части, — это в точности все простые числа.

Возьмем логарифм от обеих частей. Если что-то равно чему-то, то, конечно, и логарифм одного должен быть равен логарифму другого. Согласно 9-му правилу действий со степенями, которое гласит, что ln( a×b ) = ln а + ln b , получаем

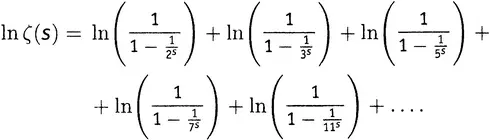
Но, поскольку ln 1/ a = −ln a согласно 10-му правилу, это выражение равно

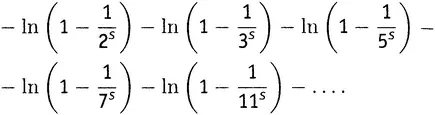
Теперь вспомним ряд сэра Исаака Ньютона для функции ln (1 − x ) из главы 9.vii. Он пригоден при x , лежащем от −1 до +1, что, без сомнения, выполнено в нашем случае, поскольку s положительно. Поэтому каждый логарифм можно разложить в бесконечный ряд таким образом (19.3):

Это бесконечная сумма бесконечных сумм — с первого взгляда, я полагаю, подобное немного пугает, но в математике такие конструкции встречаются достаточно часто.