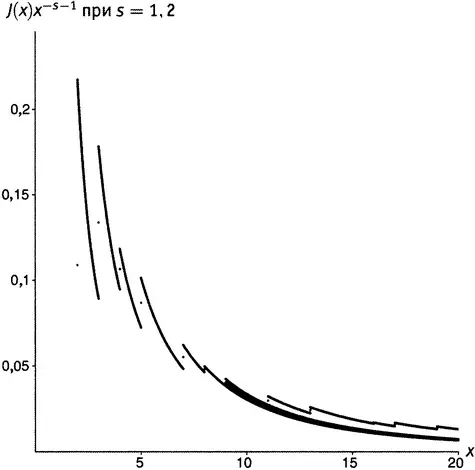
Рисунок 19.5. 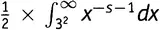 при s = 1,2.
при s = 1,2.
Давайте посмотрим. Будем перебирать простые числа одно за одним. Для простого числа 2 до сдавливания имеем полоску высоты 1, идущую от 2 до бесконечности, далее полоску высоты идущую от 2 2до бесконечности, затем полоску высоты идущую от 2 3до бесконечности, и т.д. Сумма площадей сдавленных полосок — если мы рассматриваем пока только простое число 2 — равна (19.4):
Конечно, это пока только 2-полоски. Имеется аналогичная бесконечная сумма интегралов для 3-полосок (19.5):
И аналогичная сумма для 5, потом для 7 и т.д. для всех простых чисел. Бесконечная сумма бесконечных сумм интегралов! Все хуже и хуже! Да, но самый густой мрак перед рассветом.
Это возвращает нас к началу данного раздела. Поскольку интеграл прозрачен для умножения на число , 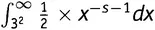 — это то же самое, что
— это то же самое, что 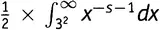 . Но в начале раздела мы видели, что член, который мы в качестве пробного выбрали в выражении (19.3), т.е.
. Но в начале раздела мы видели, что член, который мы в качестве пробного выбрали в выражении (19.3), т.е. 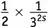 , равен
, равен 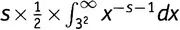 — другими словами, s умножить на то, что мы только что получили. Так к чему же сводится выражение (19.5)? Вот именно, в точности ко второй строке в выражении (19.3), деленной на s ! А выражение (19.4)плюс выражение (19.5)плюс аналогичные выражения для всех остальных простых чисел суммируются к выражению (19.3), деленному на s . Вот и рассвет! Получается, что штука, с которой я тут забавляюсь, т.е.
— другими словами, s умножить на то, что мы только что получили. Так к чему же сводится выражение (19.5)? Вот именно, в точности ко второй строке в выражении (19.3), деленной на s ! А выражение (19.4)плюс выражение (19.5)плюс аналогичные выражения для всех остальных простых чисел суммируются к выражению (19.3), деленному на s . Вот и рассвет! Получается, что штука, с которой я тут забавляюсь, т.е. 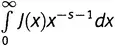 , равна просто выражению (19.3), деленному на s . Но выражение (19.3)равно ln ζ(z) , как нам подсказывает Золотой Ключ. Отсюда получается следующий результат.
, равна просто выражению (19.3), деленному на s . Но выражение (19.3)равно ln ζ(z) , как нам подсказывает Золотой Ключ. Отсюда получается следующий результат.
Золотой Ключ (аналитический вариант) (19.6)
Я просто не нахожу слов, чтобы выразить, насколько это чудесный результат. Он ведет прямо к центральному результату в работе Римана — результату, который будет предъявлен в главе 21. На самом деле это просто переписывание Золотого Ключа в терминах анализа. Однако переписать его так — это невероятно мощное достижение, потому что теперь Золотой Ключ открыт для всех мощных средств дифференциального и интегрального исчисления XIX века. В этом состояло достижение Римана.
Среди упомянутых средств обращения имеется еще один метод, который позволяет вывернуть полученное выражение наизнанку и записать J через ζ . Я немного потяну с предъявлением обращенного выражения. Но логика во всяком случае ясна:
• можно выразить π(x) через J(x) (раздел IV данной главы);
• обратив выражение (19.6), можно выразить J(x) через дзета-функцию
и, следовательно,
• можно выразить π(x) через дзета-функцию.
Именно за это предприятие Риман и взялся, потому что в результате окажется, что все свойства функции π некоторым образом закодированы в свойствах ζ -функции.
Функция π относится к теории чисел; ζ -функция относится к анализу, и мы перебросили понтонный мост через пролив, разделяющий два берега — счет и измерение. Коротко говоря, мы только что получили мощный результат в аналитической теории чисел. На рисунке 19.6 графически представлено выражение (19.6) — Золотой Ключ в аналитическом виде.
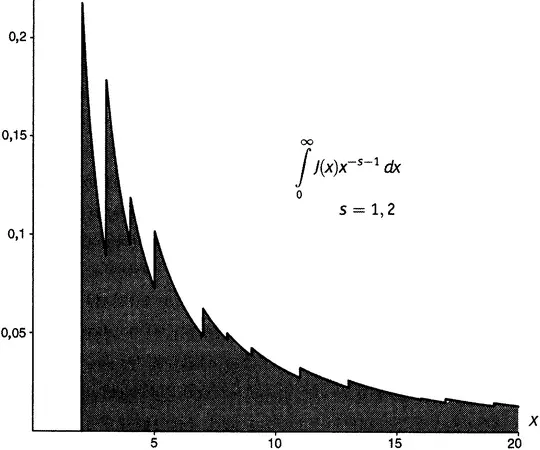
Рисунок 19.6.Затемненная область представляет собой интеграл 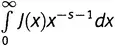 при s = 1,2. Его численное значение составляет 1,434385276163. Он равен 1/ s ∙ln ζ(s).
при s = 1,2. Его численное значение составляет 1,434385276163. Он равен 1/ s ∙ln ζ(s).
Глава 20. Риманов оператор и другие подходы
Читать дальше


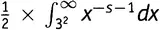 при s = 1,2.
при s = 1,2.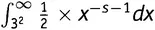 — это то же самое, что
— это то же самое, что 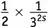 , равен
, равен 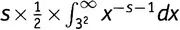 — другими словами, s умножить на то, что мы только что получили. Так к чему же сводится выражение (19.5)? Вот именно, в точности ко второй строке в выражении (19.3), деленной на s ! А выражение (19.4)плюс выражение (19.5)плюс аналогичные выражения для всех остальных простых чисел суммируются к выражению (19.3), деленному на s . Вот и рассвет! Получается, что штука, с которой я тут забавляюсь, т.е.
— другими словами, s умножить на то, что мы только что получили. Так к чему же сводится выражение (19.5)? Вот именно, в точности ко второй строке в выражении (19.3), деленной на s ! А выражение (19.4)плюс выражение (19.5)плюс аналогичные выражения для всех остальных простых чисел суммируются к выражению (19.3), деленному на s . Вот и рассвет! Получается, что штука, с которой я тут забавляюсь, т.е. 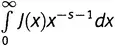 , равна просто выражению (19.3), деленному на s . Но выражение (19.3)равно ln ζ(z) , как нам подсказывает Золотой Ключ. Отсюда получается следующий результат.
, равна просто выражению (19.3), деленному на s . Но выражение (19.3)равно ln ζ(z) , как нам подсказывает Золотой Ключ. Отсюда получается следующий результат.











