Сейчас может показаться, что мы оказались в ситуации, которая много хуже той, что была вначале. Аккуратненькое бесконечное произведение мы превратили в бесконечную сумму бесконечных сумм. Предприятие может показаться безнадежным. Да, но это если не использовать всю мощь анализа.
VI.
Возьмем какой-нибудь один из членов в этой сумме сумм. Выберем, например, 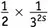 . Рассмотрим функцию x − s −1и будем временно считать, что s — положительное число. Каков интеграл от x − s −1? В силу общих правил обращения со степенями, приведенных в главе 7.vii, это x − s /(− s ), т.е. (−1/ s )×(1/ x s ). Если мы возьмем этот интеграл при x , равном бесконечности, и вычтем из того, что получится, тот же интеграл, взятый при x равном 3 2,то что получится? Ну, если x — очень большое число, то (−1/ s )×(1/ x s ) — число очень маленькое, так что справедливо будет считать, что, когда x бесконечно велико, это выражение равно нулю. И из этого — из нуля — мы собираемся вычесть (−1/ s )×(1/(3 2) s ). Такое вычитание дает (1/ s )×(1/(3 2) s ). Сухой остаток таков: выбранный член в выражении (19.3)можно переписать в виде интеграла
. Рассмотрим функцию x − s −1и будем временно считать, что s — положительное число. Каков интеграл от x − s −1? В силу общих правил обращения со степенями, приведенных в главе 7.vii, это x − s /(− s ), т.е. (−1/ s )×(1/ x s ). Если мы возьмем этот интеграл при x , равном бесконечности, и вычтем из того, что получится, тот же интеграл, взятый при x равном 3 2,то что получится? Ну, если x — очень большое число, то (−1/ s )×(1/ x s ) — число очень маленькое, так что справедливо будет считать, что, когда x бесконечно велико, это выражение равно нулю. И из этого — из нуля — мы собираемся вычесть (−1/ s )×(1/(3 2) s ). Такое вычитание дает (1/ s )×(1/(3 2) s ). Сухой остаток таков: выбранный член в выражении (19.3)можно переписать в виде интеграла
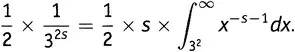
Но зачем мы вообще все это делаем? Чтобы вернуться к функции J , вот зачем.
Дело в том, что x = 3 2— это значение, при котором функция J совершает прыжок на 1/ 2. В голове у математика — и уж точно в голове у великого математика, каким был Риман, — приведенное выражение 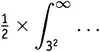 сразу вызывает некоторый образ. Этот образ представлен на рисунке 19.4: это функция J с заполненной полосой. Полоса тянется от 3 2(т.е. от 9) до бесконечности и имеет высоту одна вторая. Ясно, что вся площадь под (говорим «площадь под» — думаем «интеграл») графиком функции J составлена из подобных же полосок. Полоски высотой 1, протянувшиеся от каждого простого числа до бесконечности; полоски высотой одна вторая, идущие от каждого квадрата простого числа до бесконечности; полоски высотой одна треть от каждого куба простого числа до бесконечности… Видите, как все срастается с той бесконечной суммой бесконечных сумм в выражении (19.3)?
сразу вызывает некоторый образ. Этот образ представлен на рисунке 19.4: это функция J с заполненной полосой. Полоса тянется от 3 2(т.е. от 9) до бесконечности и имеет высоту одна вторая. Ясно, что вся площадь под (говорим «площадь под» — думаем «интеграл») графиком функции J составлена из подобных же полосок. Полоски высотой 1, протянувшиеся от каждого простого числа до бесконечности; полоски высотой одна вторая, идущие от каждого квадрата простого числа до бесконечности; полоски высотой одна треть от каждого куба простого числа до бесконечности… Видите, как все срастается с той бесконечной суммой бесконечных сумм в выражении (19.3)?
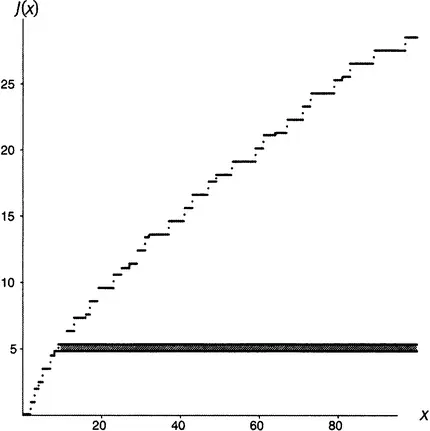
Рисунок 19.4. 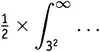 .
.
Конечно, площадь под графиком функции J бесконечна. Нарисованная полоска уже имеет бесконечную площадь (высота 1/ 2, длина бесконечна, площадь 1/ 2×∞ = ∞). Таковы же площади и всех других полосок. Все вместе они складываются в бесконечность. Но что, если я пожелаю «придавить» функцию J справа таким образом, чтобы площадь под графиком стала конечной? Так, чтобы каждая из этих полосок постепенно сужалась и сжималась до такой степени, чтобы площадь ее стала конечной? Как можно было бы осуществить такое «придавливание»?
Последний интеграл подсказывает как. Предположим, что мы взяли какое-нибудь число s (которое будем считать большим единицы). Для каждого аргумента x умножим J(x) на x − s −1. Для иллюстрации возьмем s = 1,2. Тогда x − s −1= x −2,2или, другими словами, 1/ x 2,2. Возьмем аргумент x , скажем, равным 15. Вот, J (15) есть 7,333333…, а 15 −2,2равно 0,00258582…. Перемножая, получаем, что J(x)x − s −1имеет значение 0,018962721…. Если брать большие аргументы, то сдавливание будет выражено более ярко. При x = 100 значение выражения J(x)x − s −1равно 0,001135932….
На рисунке 19.5 показан график функции J(x)x − s −1при s = 1,2. Чтобы подчеркнуть «эффект сдавливания», там показана та же самая полоска, которая была выделена и ранее, но теперь после сдавливания. Видно, как она все более и более худеет по мере того, как аргумент устремляется на восток. Имеется вполне реальный шанс, что вся площадь окажется конечной, несмотря на свою бесконечную длину. В предположении, что так и есть и что дело обстоит таким же образом для всех полосок, спросим себя: какова же будет полная площадь под графиком этой функции? Или, выражаясь математически, каково будет значение 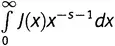 ?
?
Читать дальше

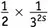 . Рассмотрим функцию x − s −1и будем временно считать, что s — положительное число. Каков интеграл от x − s −1? В силу общих правил обращения со степенями, приведенных в главе 7.vii, это x − s /(− s ), т.е. (−1/ s )×(1/ x s ). Если мы возьмем этот интеграл при x , равном бесконечности, и вычтем из того, что получится, тот же интеграл, взятый при x равном 3 2,то что получится? Ну, если x — очень большое число, то (−1/ s )×(1/ x s ) — число очень маленькое, так что справедливо будет считать, что, когда x бесконечно велико, это выражение равно нулю. И из этого — из нуля — мы собираемся вычесть (−1/ s )×(1/(3 2) s ). Такое вычитание дает (1/ s )×(1/(3 2) s ). Сухой остаток таков: выбранный член в выражении (19.3)можно переписать в виде интеграла
. Рассмотрим функцию x − s −1и будем временно считать, что s — положительное число. Каков интеграл от x − s −1? В силу общих правил обращения со степенями, приведенных в главе 7.vii, это x − s /(− s ), т.е. (−1/ s )×(1/ x s ). Если мы возьмем этот интеграл при x , равном бесконечности, и вычтем из того, что получится, тот же интеграл, взятый при x равном 3 2,то что получится? Ну, если x — очень большое число, то (−1/ s )×(1/ x s ) — число очень маленькое, так что справедливо будет считать, что, когда x бесконечно велико, это выражение равно нулю. И из этого — из нуля — мы собираемся вычесть (−1/ s )×(1/(3 2) s ). Такое вычитание дает (1/ s )×(1/(3 2) s ). Сухой остаток таков: выбранный член в выражении (19.3)можно переписать в виде интеграла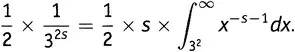
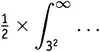 сразу вызывает некоторый образ. Этот образ представлен на рисунке 19.4: это функция J с заполненной полосой. Полоса тянется от 3 2(т.е. от 9) до бесконечности и имеет высоту одна вторая. Ясно, что вся площадь под (говорим «площадь под» — думаем «интеграл») графиком функции J составлена из подобных же полосок. Полоски высотой 1, протянувшиеся от каждого простого числа до бесконечности; полоски высотой одна вторая, идущие от каждого квадрата простого числа до бесконечности; полоски высотой одна треть от каждого куба простого числа до бесконечности… Видите, как все срастается с той бесконечной суммой бесконечных сумм в выражении (19.3)?
сразу вызывает некоторый образ. Этот образ представлен на рисунке 19.4: это функция J с заполненной полосой. Полоса тянется от 3 2(т.е. от 9) до бесконечности и имеет высоту одна вторая. Ясно, что вся площадь под (говорим «площадь под» — думаем «интеграл») графиком функции J составлена из подобных же полосок. Полоски высотой 1, протянувшиеся от каждого простого числа до бесконечности; полоски высотой одна вторая, идущие от каждого квадрата простого числа до бесконечности; полоски высотой одна треть от каждого куба простого числа до бесконечности… Видите, как все срастается с той бесконечной суммой бесконечных сумм в выражении (19.3)?
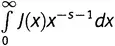 ?
?










