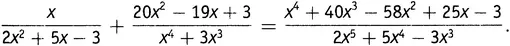Ошибкой было бы считать (как это порой делают начинающие), что конечные поля представляют собой просто переформулировку арифметики циферблата, описанной в главе 6.viii. Это верно только для полей, содержащих простое число элементов. А вот арифметика других конечных полей устроена более тонко. На рисунке 17.1, например, представлена арифметика циферблата — сложение и умножение — для циферблата с четырьмя отметками (т.е. 0, 1, 2 и 3). Эта система чисел и правил интересна и полезна, но она не является полем, поскольку нельзя разделить 1 ни на 3, ни на 2. (Если бы можно было разделить 1 на 2, то уравнение 1 = 2× x имело бы решение. А у него решения нет.) Математики называют это кольцом , что не лишено основания, коль скоро речь идет о циферблате. В кольце можно складывать, вычитать и умножать, но не всегда можно делить.
| + |
0 |
1 |
2 |
3 |
|
× |
0 |
1 |
2 |
3 |
| 0 |
0 |
1 |
2 |
3 |
0 |
0 |
0 |
0 |
0 |
| 1 |
1 |
2 |
3 |
0 |
1 |
0 |
1 |
2 |
3 |
| 2 |
2 |
3 |
0 |
1 |
2 |
0 |
2 |
0 |
2 |
| 3 |
3 |
0 |
1 |
2 |
3 |
0 |
3 |
2 |
1 |
Рисунок 17.1.Сложение и умножение на циферблате с четырьмя отметками (другими словами, сложение и умножение выполняются по обычным правилам, после чего берутся остатки по модулю 4).
Конкретное кольцо, показанное на рисунке 17.1, имеет официальное обозначение Z/4 Z. Должен сознаться, что мне такое обозначение никогда не нравилось, так что на правах автора я изобрету для него свое собственное обозначение: CLOCK 4. [158] {4} Ясно, что можно построить такое кольцо для любого натурального числа N. В моих обозначениях оно будет называться CLOCK N .
Но поле F N можно построить не для любого числа N , а только для простых чисел и их степеней. Для простого числа p самого по себе поле F p выглядит в точности как CLOCK p — та же таблица сложения, та же таблица умножения. Однако для степени простого числа ситуация усложняется. На рисунке 17.2 показаны сложение и умножение (откуда, конечно, извлекаются вычитание и деление) в поле F 4. Видно, что F 4отличается от CLOCK 4.
| + |
0 |
1 |
2 |
3 |
|
× |
0 |
1 |
2 |
3 |
| 0 |
0 |
1 |
2 |
3 |
0 |
0 |
0 |
0 |
0 |
| 1 |
1 |
0 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
| 2 |
2 |
3 |
0 |
1 |
2 |
0 |
2 |
3 |
1 |
| 3 |
3 |
2 |
1 |
0 |
3 |
0 |
3 |
1 |
2 |
Рисунок 17.2.Сложение и умножение в конечном поле F 4.
Всякое поле, конечное или бесконечное, имеет важный параметр — число, называемое характеристикой. Характеристика поля говорит о том, сколько раз надо прибавить единицу к самой себе, чтобы получить нуль. Если 1 + 1 + 1 + … = 0 (где берется N слагаемых), то характеристика равна N. Понятно, что характеристика поля F 2равна 2. Чуть менее очевидно, хотя и без труда проверяется с помощью таблицы сложения на рисунке 17.2, то, что характеристика поля F 4тоже равна 2. Такие поля, как Q, R, С, в которых никакое прибавление единицы к самой себе какое угодно количество раз никогда не даст в результате нуль, по определению имеют характеристику «нуль». (Вы могли бы подумать, что более логичной будет характеристика «бесконечность», и вы, возможно, правы, но имеются веские причины и для того, чтобы объявить характеристику нулевой.) Можно проверить, что характеристика любого поля есть или нуль, или некоторое простое число.
Поскольку мы имеем дело с алгеброй, элементы полей не обязаны быть числами. Алгебра позволяет работать с математическими объектами любого типа. Рассмотрим все многочлены (полиномиальные функции) любой заданной степени, т.е. все выражения вида ax n+ bx n−1+ cx n−2+ … , где a, b, c и т.д. — целые числа. Теперь образуем множество всех рациональных функций, другими словами, функций, являющихся отношением (ratio) двух многочленов. Получим поле. Приведем пример сложения в этом поле:
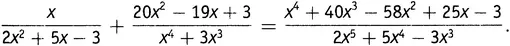
(Примерно этим и занимаются на уроках алгебры в старших классах.)
Читать дальше