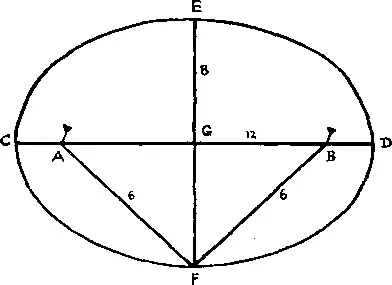
301. Проведите два перпендикулярных отрезка CD и EF (длина CD равна 12 см, длина EF — 8 см), пересекающихся друг с другом посередине. Найдите такие точки A и B , чтобы AF и FB равнялись половине CD , то есть 6 см, и поместите ваши булавки в A и B , взяв веревочную петлю равной ABFA . Пусть CA = x . Тогда, если карандаш находится в F , длина веревки равна 12 + (12 - 2 x ) = 24 - 2 x , а если он находится в C , длина веревки равна тоже 2(12 - x ) = 24 - 2 x , что и доказывает правильность нашего решения [39] Строго говоря, это еще не доказательство, но его можно легко получить, пользуясь свойствами эллипса. Булавки должны располагаться в фокусах эллипса A к B . CD представляет собой большую, a EF — малую оси эллипса; обозначим их соответственно через 2 a и 2 b , а фокусное расстояние AB через 2 c . Тогда из треугольника AGF получим AF = . Но в силу свойств эллипса = a , то есть AF = CD , что и требовалось. — Прим. перев.
.

302. Одного взгляда на помещенный здесь рисунок достаточно, чтобы заметить, что если я отрежу часть 1 и помещу ее на место части 2 , то получится прямой отрезок стены BC , отмеченный пунктиром и в точности равный участку AB . Следовательно, не правы были оба спорщика, и цена обоих участков должна быть одинаковой. Конечно, читатель сразу заметит, что это справедливо лишь при некоторых ограничениях, но мы имеем в виду именно ту стену, какая нарисована, и в том случае, когда эти ограничения выполнены.
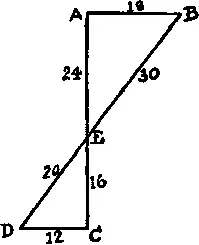
303. Отмерьте любое удобное расстояние вдоль берега от A до C , скажем 40 м. Затем отмерьте любое расстояние в перпендикулярном направлении до точки D , скажем 12 м. Теперь сделайте засечку E в направлении AB . Вы сможете измерить расстояние от A до B , которое в нашем случае равно 24 м, и от E до C , что даст 16 м. Далее, AB : DC = AE : EC , откуда ясно, что ширина реки AB равна 18 м.
304. Свинья пробежит 66⅔ м и будет схвачена, а Пэт пробежит 133⅓ м. Кривую [40] Эта кривая называется линией погони. — Прим. перев.
, которую опишет при этом Пэт, можно измерить точно. Ее длина равна an 2/( n 2- 1), где скорость свиньи принята за 1, Пэт бежит в n раз быстрее и a — первоначальное расстояние между Пэтом и свиньей.
305. Расстояние от верхнего конца до земли составляет ⅘ длины всей лестницы. Умножьте расстояние от стены (4 м) на знаменатель этой дроби (5), и вы получите 20. Теперь вычтите квадрат числителя дроби ⅘ из квадрата ее знаменателя. При этом получится 9 = 3 2. Наконец, разделите 20 на 3, и вы получите ответ: 6 м.
306. Высота шеста над землей составляла 50 м. В первом случае он сломался в 29 м, а во втором случае в 34 м от верхушки.
307. Длина свободно висящей веревки равна 3 м 85½ см.
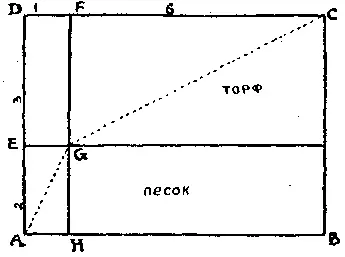
308. Разумеется, прямая AC не является наибыстрейшим путем. Быстрее будет доехать от A до E и далее прямо до C . Путь, требующий наименьшей затраты времени, показан на рисунке пунктирной линией от A до G (ровно 1 км от E ) и затем прямо до C .
Необходимо, чтобы синус угла FGC был в два раза больше синуса угла AGH , В первом случае синус равен 6/ 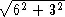 = 6
= 6 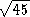 = 2/ . Во втором случае синус равен 1/
= 2/ . Во втором случае синус равен 1/ 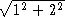 = 1/ , то есть ровно в два раза меньше.
= 1/ , то есть ровно в два раза меньше.
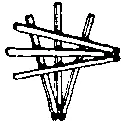
309. Как видно из рисунка, головоломка невероятно проста, если знаешь, как к ней подступиться! И все же у меня нет ни малейшего сомнения, что для многих читателей она оказалась крепким орешком. Можно заметить, что каждая спичка, несомненно, касается всех остальных.
Читать дальше





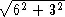 = 6
= 6 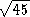 = 2/ . Во втором случае синус равен 1/
= 2/ . Во втором случае синус равен 1/ 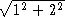 = 1/ , то есть ровно в два раза меньше.
= 1/ , то есть ровно в два раза меньше.






![О Генри - Через двадцать лет [After Twenty Years]](/books/415401/o-genri-cherez-dvadcat-let-after-twenty-years-thumb.webp)

