Генри Дьюдени - Пятьсот двадцать головоломок

[Это решение было впервые найдено английским математиком-любителем Генри Перигейлом, который опубликовал его в 1873 г. Оно представляет собой одно из лучших доказательств теоремы Пифагора с помощью разрезания. См. гл. 38 книги М. Гарднера «Математические головоломки и развлечения» (М., изд-во «Мир», 1971). — М. Г. ].

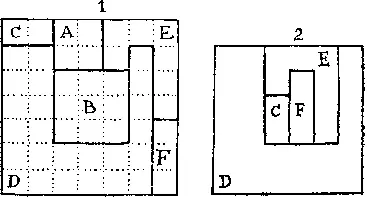
348. На рисунке показано, как можно разрезать фанеру. Квадраты A и B вырезаются целиком (1) , а из четырех частей C , D , E и F можно составить третий квадрат (2) .

[Существуют решения данной задачи, в которых участвует только пять частей. Не сможет ли читатель отыскать решение из пяти частей, при котором общая длина разрезов составляет 16 единиц? — М. Г. ]

349. Вырежьте кусок A и, повернув его на четверть оборота по часовой стрелке, соедините с куском B . При этом получится правильная шахматная доска.

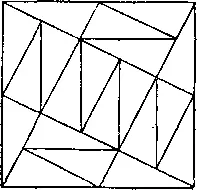
350. На рисунке показано, как составить квадрат из 20 кусочков.

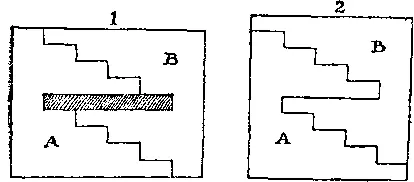
351. Если ковер разрезать на две части, как показано в случае 1 , и сшить куски вместе таким образом, как изображено в случае 2, то получится квадрат. Ширина ступеньки равна 2, а высота 1 м.

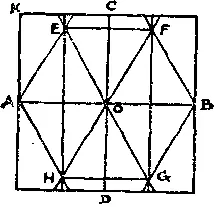
352. Согнув листок по серединам противоположных сторон, получим прямые AOB и COD . Произведем также сгибы EH и FG , делящие AO и OB пополам. Перевернем AK так, чтобы K попала на прямую EH в точке E , а затем произведем сгибы через AE и EOG . Аналогично найдем точку H и согнем бумагу вдоль AH и HOF . Произведя сгибы BF , BG , EF и HG , получим искомый правильный шестиугольник EFBGHAE .

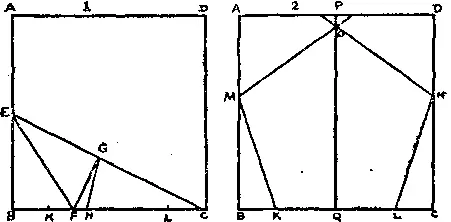
353. Сложив AB вдвое, найдите середину E . Согните бумагу вдоль EC . Совместите EB с EC и согните так, чтобы получить EF и FG . Сделайте так, чтобы отрезок CH стал равным отрезку CG . Найдите K — середину отрезка BH и отложите отрезок CL , равный BK . Отрезок KL — сторона правильного пятиугольника. Затем отложите (см. правую часть рисунка) отрезки KM и LN , равные KL , так, чтобы M и N соответственно лежали на BA и CD . Согнув бумагу вдоль PQ , отложите MO и NO , равные KM и LN . Многоугольник KMONL и есть искомый пятиугольник.

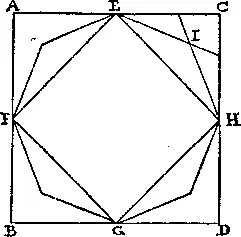
354. Соединив между собой края AB и CD , вы можете отметить сгибами средние точки E и G . Аналогичным образом вы можете найти точки F и H , а затем согнуть квадрат EHGF . Далее совместите CH с EH и EC с EH , при этом вы получите точку пересечения 1 . Сделайте то же самое с оставшимися тремя углами — сгибы очертят правильный восьмиугольник, который затем можно будет вырезать с помощью ножниц.

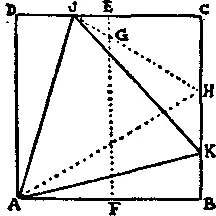
355. Сложите квадрат пополам вдоль FE . Загните сторону AB так, чтобы точка B легла на FE , и вы получите точки G и H , через которые можно провести сгиб HGJ . Оставляя точки B и G по-прежнему совмещенными, отогните AB назад на AH , и вы получите прямую AK . Теперь вы можете сложить треугольник AJK — наибольший равносторонний треугольник из всех возможных.

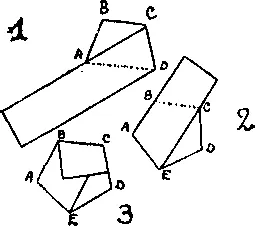
356. Отогнув угол A , найдите точку C , которая делала бы отрезок BC равным отрезку AB , и перегните полоску, как показано в случае 1 . Вы получите точку D . Далее согните полоску так, как показано в случае 2 , чтобы ее край прошел вдоль AB . Вы получите точку E . Продолжая действовать аналогичным образом (случай 3 ), вы уложите всю полоску в форме пятиугольника. Это, как мы уже говорили, просто, но вместе с тем интересно и поучительно.