Второе свойство, которое я потребовал от значительной идеи, - её глубина. Определить его ещё труднее. Оно каким-то образом связано с трудностью; "более глубокие" идеи обычно труднее постичь, но вместе с тем это не одно и то же. Идеи, лежащие в основании теоремы Пифагора и её обобщений весьма глубоки, но современный математик не счёл бы их трудными. С другой стороны, теорема может быть в сущности поверхностна, но очень трудна для доказательства (таковы, например, очень многие "диофантовы"[ 120 120 Диофант (ок 250) - математик эпохи эллинизма. Сохранились два его сочинения: "Арифметика" и "О многоугольных числах".
] теоремы, т.е. теоремы о решении уравнений в целых числах).
Создаётся впечатление, что математические идеи "стратифицированы", т.е. расположены как бы слоями, идеи в каждом слое связаны целым комплексом отношений между собой и с идеями, лежащими в верхних и нижних слоях. Чем ниже слой, тем глубже (и, как правило, труднее) идея. Так, идея "иррационального числа" глубже идеи целого числа, и по этой причине теорема Пифагора глубже теоремы Евклида.
Сосредоточим внимание на отношениях между целыми числами или в какой-нибудь другой группе объектов, лежащих в каком-нибудь конкретном слое. Может случиться так, что одно из этих отношений окажется полностью понятным, что мы сможем распознать и доказать, например, какое-нибудь свойство целых чисел, не зная о содержании слоев, расположенных ниже. Так, теорему Евклида мы доказали, рассматривая только свойства целых чисел. Но существует также немало теорем о целых числах, которые мы не можем должным образом оценить и ещё в меньшей степени доказать, не "копая" глубже и не выясняя того, что происходит в лежащих ниже слоях.
Нетрудно привести соответствующие примеры из теории простых чисел. Теорема Евклида очень важна, но не отличается особой глубиной: мы можем доказать, что существует бесконечно много простых чисел, не пользуясь ничем глубже понятия "делимости". Но как только мы узнаем, что простых чисел бесконечно много, сразу же возникают новые вопросы. Да, простых чисел бесконечно много, но как они распределены? Пусть N - некоторое большое число, например, 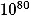 или
или 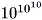 (
( 13 13 Предполагается, что во всей Вселенной содержится около 1080 протонов. Число 101010, если его записать в развернутом виде, заняло бы около 50000 томов средней величины.
). Сколько существует простых чисел, не превосходящих числа N?( 14 14 В %14 я упомянул о том, что существует 50847478 простых чисел, не превосходящих числа 1000000000, но это предел, до которого простирается наше точное значение.
) Стоит нам задать эти вопросы, как мы оказываемся в совершенно ином положении. Мы в состоянии ответить на них с поразительной точностью, но только если копнем глубже, оставив на время в стороне целые числа, и воспользуемся самым мощным оружием современной теории функций. Таким образом, теорема, дающая ответ на наши вопросы (так называемая "теорема о распределении простых чисел"), гораздо глубже теоремы Евклида или даже теоремы Пифагора.
Я мог бы легко увеличить число примеров, но понятие "глубины" неуловимо даже для математика, способного его распознать, и вряд ли я могу сказать ещё что-нибудь об этом понятии, что будет особенно полезным читателям-неспециалистам.
Есть ещё один вопрос, оставшийся после §11, где я позволил себе сравнить "настоящую" математику и шахматы. Мы можем считать теперь не подлежащим сомнению, что по самой своей сути, серьёзности и значимости настоящая математическая теорема имеет подавляющее преимущество перед шахматами. Для тренированного интеллекта почти столь же очевидно, что настоящая математика обладает большим преимуществом и в красоте, но это преимущество гораздо труднее определить или указать его местоположение, так как основной дефект шахматной задачи заключается просто в её "тривиальности", и контраст в этом отношении смешивается с любым чисто эстетическим соображением и возмущает последнее. Какие "чисто эстетические" свойства мы можем обнаружить в таких теоремах, как теорема Евклида и теорема Пифагора? Я рискну сделать лишь несколько разрозненных замечаний.
И та и другая теорема (разумеется, в теоремы я включаю не только формулировки, но и доказательства) отличаются весьма высокой степенью неожиданности в сочетании с непреложностью и экономичностью. Доказательства необычны и удивительны по форме; используемые инструменты кажутся по-детски простыми по сравнению с далеко идущими результатами, но все заключения с необходимостью вытекают из теоремы. Детали не загромождают основную линию доказательства - в каждом случае достаточно атаковать только в одном направлении. То же самое относится и к доказательству многих гораздо более трудных теорем. Чтобы оценить их по достоинству, требуются весьма основательные познания в математике. "Многовариантность" доказательства математической теоремы отнюдь не требуется: перечисление всех случаев - одна из наиболее скучных форм математического доказательства. Математическое доказательство должно напоминать созвездие с ясными и чёткими очертаниями, а не скопление звёзд с размытыми границами в Млечном Пути.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

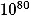 или
или 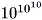 (
(