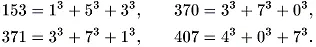Годфри Харди. - Апология математика

(а) 8712 и 9801 единственные четырёхзначные числа, равные целым кратным числам, полученным при записи в обратном порядке:

Других чисел, не превосходящих 10000, которые бы обладали этим свойством, не существует.

(б) Существуют только четыре числа (кроме 1), равных сумме кубов цифр, например,

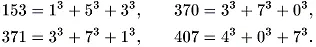
Все это забавные факты, весьма подходящие для газетных колонок с головоломками, способные позабавить любителей, но ничего в них не затронет сердце математика. Их доказательства не трудны и не интересны, а всего лишь немного утомительны. Соответствующие утверждения, как теоремы, не серьёзны. Ясно, что одна из причин этого (хотя, вероятно, не самая важная) - чрезмерная конкретность как формулировок, так и доказательств, не допускающих никаких обобщений.

"Общность" - многозначное и весьма опасное слово, и мы должны тщательно следить за тем, чтобы оно не слишком доминировало в наших обсуждениях. Оно используется в различных смыслах и в математике и в литературе о математике, и на общности, понимаемой в одном из смыслов, логики делают особый акцент, хотя для нас такое понимание логиков здесь полностью неуместно. В этом смысле, как нетрудно доказать, все математические теоремы обладают одинаковой и полной "общностью".

"Определённость математики, - говорит Уайтхед, - зависит от её совершенно абстрактной общности". Когда мы утверждаем, что 2+3=5, мы говорим об отношении между тремя группами "вещей", и эти "вещи" - не яблоки, монеты или вещи того или иного вполне определённого рода, а просто "вещи", "любые виды вещей". Смысл утверждения совершенно не зависит от индивидуальностей членов групп. Все математические "объекты", "сущности" или "отношения", такие, как "2", "3", "5", "+" или "=", и все математические предложения, в которые они входят, носят совершенно общий характер в том смысле, что они совершенно абстрактны. Одно из слов в утверждении Уайтхеда излишне, так как общность в этом смысле есть абстрактность.

Этот смысл слова "общность" важен, и логики поступают вполне справедливо, подчёркивая его, так как он воплощает в себя трюизм, о котором весьма многие из тех, кто должен был бы разбираться в этом лучше, склонны забывать. Например, нередко приходится слышать, как какой-нибудь астроном или физик заявляет, будто ему удалось найти "математическое доказательство" того, что физическая Вселенная должна вести себя так, а не иначе. Все такие заявления, если интерпретировать их буквально, представляют собой абсолютный нонсенс. Невозможно доказать математически, что завтра произойдёт солнечное или лунное затмение потому, что затмения и другие физические явления не входят в качестве составных частей в абстрактный мир математики. Я убеждён, что все астрономы были бы вынуждены признать правильность этого утверждения, сколько бы затмений они ни предсказали до этого.

Ясно, что сейчас нас интересует "общность" иного рода. Мы ищем различия в общности математических теорем, которые в смысле Уайтхеда все обладают одинаковой общностью. Таким образом, "тривиальные" теоремы (а) и (в) из §15 столь же "абстрактны" или "общи", как теоремы Евклида и Пифагора и как любая шахматная задача. Для шахматной проблемы безразлично, какого цвета фигуры - белые и чёрные или красные и зелёные и, вообще, существуют ли физические "фигуры". Во всех этих случаях мы имеем дело с одой и той же задачей, которую знаток легко держит в голове, а нам приходится трудолюбиво воспроизводить на шахматной доске. Нужно сказать, что шахматная доска и фигуры - всего лишь устройства, стимулирующие наше вялое воображение и имеющие к сути проблемы ничуть не больше отношения, чем доска и мел - к теоремам, доказываемым на лекции по математике.

Речь идёт не о той общности, которая присуща всем математическим теоремам, поиском которой мы занимались до сих пор. Сейчас нас интересует та, более тонкая и неуловимая, общность, которую я попытался в общих чертах описать в §15. И нам следует тщательно следить за тем, чтобы не делать чрезмерный акцент даже на такой общности (как это имеют обыкновение делать логики, например, Уайтхед). Это не просто "нагромождение тонкостей обобщения на тонкости обобщения", принадлежащее к числу выдающихся достижений современной математики. Некоторая мера общности должна присутствовать в любой теореме высокого класса, но чрезмерная дозировка общности неизбежно приводит к "бесцветности" теоремы. "Всё есть то, что оно есть, а не другое", и различия между вещами не менее интересны, чем сходство между ними. Мы выбираем своих друзей не потому, что они воплощают в себя все приятные качества, какие только могут быть присущи людям, а потому, что они являются теми, кто они есть. Так происходит и в математике; свойство, общее для слишком многих объектов, вряд ли может быть очень интересным, и математические идеи также становятся скучными, если не обладают индивидуальностью в достаточной мере. Здесь я по крайней мере могу процитировать Уайтхеда, выступающего в данном случае на моей стороне: "Плодотворная концепция заключается в широком обобщении, ограниченном удачной конкретизацией".