Яков Перельман - Живая математика. Математические рассказы и головоломки

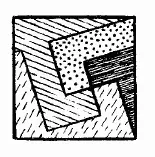
Рис. 143

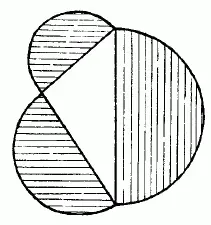
Рис. 144

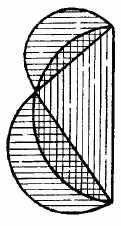
Рис. 145

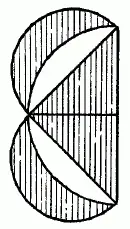
Рис. 146

116. Читатели, слыхавшие о неразрешимости задачи квадратуры круга, сочтут, вероятно, и предлагаемую задачу неразрешимой строго геометрически. Раз нельзя превратить в равновеликий квадрат полный круг, то, думают многие, нельзя превратить в прямоугольную фигуру и луночку, составленную двумя дугами окружности. Между тем задача, безусловно, может быть решена геометрическим построением, если воспользоваться одним любопытным следствием общеизвестной Пифагоровой теоремы.

Следствие, которое я имею в виду, гласит, что сумма площадей полукругов, построенных на катетах, равна полукругу, построенному на гипотенузе (рис. 144).Перекинув большой полукруг на другую сторону (рис. 145).видим, что обе заштрихованные луночки вместе равновелики треугольнику [38] Положение это известно в геометрии под названием «теоремы о Гиппократовых луночках». .

Если треугольник взять равнобедренный, то каждая луночка в отдельности будет равновелика половине этого треугольника (рис. 146).

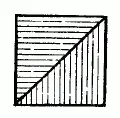
Рис. 147

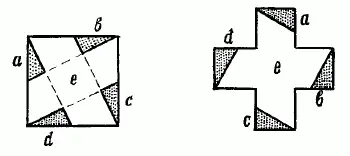
Рис. 148. Превращение квадрата в крест

Отсюда следует, что можно геометрически точно построить равнобедренный прямоугольный треугольник, площадь которого равна площади серпа. А так как равнобедренный прямоугольный треугольник легко превращается в равновеликий квадрат (рис. 147)»то и серп наш возможно чисто геометрическим построением заменить равновеликим квадратом.

Остается только превратить этот квадрат в равновеликую фигуру Красного Креста (составленную, как известно, из 5 примкнутых друг к другу равных квадратов). Существует несколько способов выполнения такого построения; два из них показаны на рис. 148и 149.

Оба построения начинают с того, что соединяют вершины квадрата с серединами противоположных сторон. Важное замечание: превратить в равновеликий крест можно только такую фигуру серпа, которая составлена из двух дуг окружностей: наружного полукруга и внутренней четверти окружности соответственно большего радиуса [39] Тот лунный серп, который мы видим на небе, имеет несколько иную форму: его наружная дуга – полуокружность, внутренняя же – полуэллипс. Художники часто изображают лунный серп неверно, составляя его из дуг окружностей. .

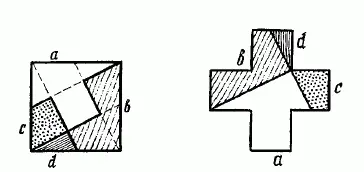
Рис. 149. Другой способ превращения квадрата в крест

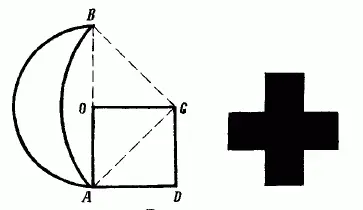
Рис. 150

Итак, вот ход построения креста, равновеликого серпу. Концы Аи Всерпа (рис. 150)соединяют прямой: в середине О этой прямой восставляют перпендикуляр и откладывают ОС=ОА.Равнобедренный треугольник ОАСдополняют до квадрата ОАDС,который превращают в крест одним из способов, указанных на рис. 148и 149.

117. Приводим окончание прерванного рассказа Бенедиктова:

«Задача была мудреная. Дочери, идучи на рынок, стали между собой совещаться, причем вторая и третья обращались к уму и совету старшей. Та, обдумав дело, сказала:

- Будем, сестры, продавать наши яйца не десятками, как это делалось у нас до сих пор, а семерками: семь яиц - семерик; на каждый семерик и цену положим одну, которой все и будем крепко держаться, как мать сказала. Чур, не спускать с положенной цены ни копейки! За первый семерик алтын 1, согласны?

- Дешевенько, - сказала вторая.

- Ну, - возразила старшая, - зато мы поднимем цену на те яйца, которые за продажею круглых семериков в корзинах у нас останутся. Я заранее проверила, что яичных торговок, кроме нас, на рынке никого не будет. Сбивать цены некому; на оставшееся же добро, когда есть спрос, а товар на исходе, известное дело, цена возвышается. Вот мы на остальных-то яйцах и наверстаем.