Тем не менее, если бы они расположились максимально нерационально , то есть всегда оставляя возле себя свободное место (и оставив свободное место в каждом ряду у прохода: на одном или на другом конце ряда, как показано на рисунке ниже), то пустовала бы одна треть мест, потому что каждая пара заняла бы три места: два для себя и одно промежуточное.
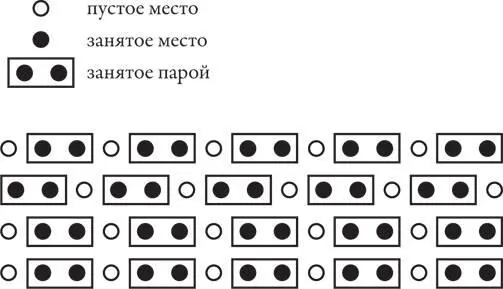
Догадываясь, что произвольный выбор должен лежать где-то между идеально рациональным и совершенно неэффективным, иначе говоря, быть средним между 0 и 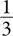 , мы ожидаем что-то около
, мы ожидаем что-то около 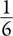 , то есть что 16,7 % мест будут пустовать. И это недалеко от точного результата 13,5 %.
, то есть что 16,7 % мест будут пустовать. И это недалеко от точного результата 13,5 %.
Здесь большое число вариантов возникло из-за того, что у пар был богатый выбор в огромном кинотеатре. Наш следующий пример тоже об организации пар, только теперь не в пространстве, а во времени. То, о чем я говорю, касается довольно болезненной проблемы: со сколькими партнерами я должен встретиться прежде, чем выберу себе супругу [100] Вопрос о том, когда прекращать перебирать партнеров и останавливать выбор на будущем супруге, изучался в различных формах и имеет различные названия: задача о невесте, задача о вступлении в брак, задача о капризном поклоннике, задача о выкупе султана за невесту. Но наиболее распространенное в настоящее время название — это задача секретаря. (Воображаемый сценарий найма лучшего секретаря из данного списка кандидатов. Вы беседуете с каждым претендентом по отдельности и должны решить, берете ли вы его на работу или прощаетесь навсегда). Для ознакомления с этой замечательной математической головоломкой и ее историей см. http://mathworld.wolfram.com/SultansDowryProblem.html и http://en.wikipedia.org/wiki/Secretary_problem. Для дополнительных сведений обратитесь к статье T. S. Ferguson, Who solved the secretary problem? Statistical Science, Vol. 4, № 3 (1989), pp. 282–289. Понятное изложение решения этой задачи можно найти по адресу http://www.math.uah.edu/stat/urn/Secretary.html. Для лучшего ознакомления с теорией оптимальных правил остановки см. T. P. Hill, Knowing when to stop: How to gamble if you must — the mathematics of optimal stopping, American Scientist, Vol. 97 (2009), pp. 126–133.
. Реальный вариант этой задачи слишком сложен для математического расчета. Рассмотрим упрощенную модель. Несмотря на допущения, невозможные в жизни, в ней все еще сохраняется некоторая душераздирающая романтическая неопределенность.
Предположим, вам известно, сколько потенциальных супругов вы встретите в течение жизни. (Фактическое количество не важно, лишь бы знать наперед, сколько их будет, и чтобы не слишком мало).
Предположим также, что вы могли бы оценить этих людей однозначно (то есть выбрать наилучшего), если бы увидели их всех вместе. К несчастью, это невозможно. Вы встречаете их только по одному и в случайном порядке. Таким образом, вы не можете знать, находится ли предмет ваших мечтаний с первым номером из вашего списка прямо за углом или вы уже встречались и расстались.
И правила этой игры таковы: как только вы позволите кому-то уйти, он (или она) тут же уходит. Второго шанса нет.
Наконец представим, что вы хотите остепениться. В этом случае, если вы порываете с тем «наилучшим на сегодняшний день», кого в прошлом не поместили в верхнюю часть списка, вы будете считать свою личную жизнь неудачной.
Есть ли надежда найти истинную любовь? Если да, то что нужно сделать, чтобы обеспечить себе наибольшие шансы?
Хорошая стратегия, хотя и не самая оптимальная, — разделить свою жизнь с момента, когда у вас начались романтические отношения, и до настоящего времени на две равные части. В первой половине вы мужчина нарасхват [101] «Мужчина нарасхват» — кинофильм режиссера Габриэле Муччино (2012). Звезда футбола и просто шикарный мужчина (Джерард Батлер) по воле случая становится тренером детской футбольной команды. С этого момента для своих подопечных и их обольстительных мамочек он мужчина нарасхват. Прим. перев.
, а во второй — готовы к серьезным отношениям и собираетесь схватить первого же партнера, который будет лучше тех, с кем вы встречались до этого.
Следуя такой стратегии, есть по крайней мере 25-процентный шанс найти предмет мечтаний. И вот почему: шансов встретить его во второй половине жизни, когда вы созрели для серьезных отношений, у вас 50 на 50, и столько же встретить наилучшего на сегодня в первой половине жизни, когда вы еще легкомысленны. Вероятность, что произойдут оба события, составляет 25 %. В этом случае вы найдете свою истинную любовь.
Читать дальше


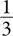 , мы ожидаем что-то около
, мы ожидаем что-то около 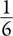 , то есть что 16,7 % мест будут пустовать. И это недалеко от точного результата 13,5 %.
, то есть что 16,7 % мест будут пустовать. И это недалеко от точного результата 13,5 %.





![Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]](/books/438782/stiven-strogac-beskonechnaya-sila-kak-matematicheski-thumb.webp)



