Антонио Дуран - Истина в пределе. Анализ бесконечно малых

Производная функции f в точке а показывает, как изменится функция в этой точке по сравнению с тем, как изменяется значение переменной. Рассмотрим две функции из прошлых примеров: s(t) = √t и v(t) = t 2. При t = 1 обе эти функции принимают значение 1: s(l) = 1 и v(1) = 1. Однако из таблицы значений видно, что поведение функций вблизи t = 1 существенно различается:

Заметьте, что функция v вблизи 1 изменяется более резко, чем функция s.

Чтобы измерить эти изменения, то есть чтобы определить производную, выберем произвольное число а и близкое к нему число a + h. Рассмотрим, как изменяется значение функции в этих точках по сравнению с изменением значения переменной. Для этого разделим разность значений функции f(a + h) — f(а) на разность значений переменных, а + h — a = h. Искомая дробь будет иметь вид:

Продолжим рассматривать функции s(t) = √t и v(t) = t 2 . Вычислим значения этой дроби для а = 1:

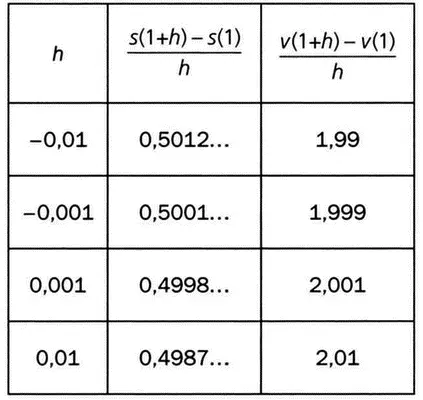
Наибольшее значение этой дроби для функции v приближается к 2, для функции s оно примерно равно 0,5. Это указывает на все тот же факт, который можно видеть из предыдущей таблицы: функция v вблизи точки 1 изменяется быстрее, чем функция s. Нас особенно интересует значение дроби

при h = 0, то есть когда числа а + h и а совпадают. Это значение мы назовем производной функции f в точке а. Будем обозначать его f’(а). Это обозначение ввел французский математик Жозеф Луи Лагранж (1736—1813) (см. главу 6). Как можно видеть, значение этой дроби равно 0/0, то есть оно не определено.

Однако это лишь кажущаяся неопределенность, поскольку, как показано в предыдущей таблице, для наших функций s(t) = √t и v(t) = t 2 при малых значениях h, отличных от нуля, обе дроби

определены и равны соответственно 0,5 для функции s(t) = √t и 2 — для функции v(t) = t 2. Далее мы покажем, что эти значения действительно соответствуют значениям производных обеих функций в точке 1, то есть s’(l) = 0,5 и v’(l) = 2.

Деление ноля на ноль, возникающее при определении производной, представляло трудность для ученых XVII века и их предшественников всякий раз, когда они пытались рассчитать, например, угол наклона касательной к кривой или мгновенную скорость движения тела, зная пройденный им путь.

Бесконечность, основа анализа бесконечно малых, скрывается именно в этой операции деления ноля на ноль. Как мы только что сказали, нас интересует значение дроби

при h = 0, когда и числитель, и знаменатель обращаются в ноль. Подобные величины, равные нулю, отношение которых необходимо найти, математики XVII века назвали бесконечно малыми.

Анализ бесконечно малых, созданный Ньютоном и Лейбницем и усовершенствованный Леонардом Эйлером (1707—1783) и другими математиками XVIII века, можно назвать искусством манипулирования бесконечно малыми величинами. Как рассказывается в следующих главах, парадоксально, но ни один из этих гениальных математиков не определил сколько-нибудь точно понятие бесконечно малой величины, которое легло в основу математического анализа.

Ньютону и Лейбницу удалось завершить работу множества их коллег — математиков XVII века и создать анализ бесконечно малых, одним из разделов которого является дифференциальное исчисление. Ньютон и Лейбниц определили простые правила, позволявшие устранять неопределенность, которая заключается в делении ноля на ноль и возникает всякий раз, когда мы хотим вычислить производную функции. Это были правила вычисления производных элементарных функций, в частности степенной:

тригонометрических функций:

логарифмов:

показательных функций:

а также правила вычисления производной для основных операции с функциями, в частности суммы:

произведения:

деления:

и для сложных функций:

Гордиевым узлом анализа бесконечно малых на протяжении XVII, XVIII и начала XIX века оставалось четкое определение того, как следует понимать значение дроби