Стюарт Исакофф - Музыкальный строй. Как музыка превратилась в поле битвы величайших умов западной цивилизации

Мнение Винченцо Галилея о музыкальном строе недалеко ушло от наставлений Бруно: избавьтесь от гнета канонов, советовал тот, ведь нет никаких правил, кроме тех, что вы установите сами. Свои идеи – а также свое недоверие к официальным доктринам – Галилей передал по наследству и родному сыну, Галилео. “Я не обязан верить, что один и тот же Бог одарил нас чувствами, здравым смыслом и разумом – и при этом требует, чтобы мы отказались от их использования”, – как-то сказал он. Правда, в конце жизни Галилео Галилею пришлось предстать перед римскими властями в белых одеждах кающегося грешника и затем, по требованию инквизиции, публично развенчать утверждение Коперника о том, что Земля вращается вокруг Солнца.

Наука и музыка к этому времени уже давно шли рука об руку – правда, музыкальные воззрения Галилея не были слишком радикальными и не наносили чрезмерный ущерб церковным доктринам. И все же даже они казались вызывающими. Бруно возражал церкви, провозглашая Вселенную бесконечной; Винченцо Галилей возражал Царлино, вводя в музыкальную вселенную бесконечные дробные числа. Если его отец был прав, утверждая, что гаммы рукотворны и не являются продуктом “звучащего числа” Царлино, вопрошал Галилео, то почему же некоторые сочетания тонов заставляют небеса улыбаться, а другие – хмуриться? Наверняка, полагал он, у этого феномена должно быть научное объяснение. Именно так он пришел к своей теории консонанса, сформулировав ее по итогам наблюдения за качающимися маятниками. Правда, его коллега-философ и убежденный сторонник равномерной темперации Джованни Баттиста Бенедетти пришел к похожим выводам еще раньше.

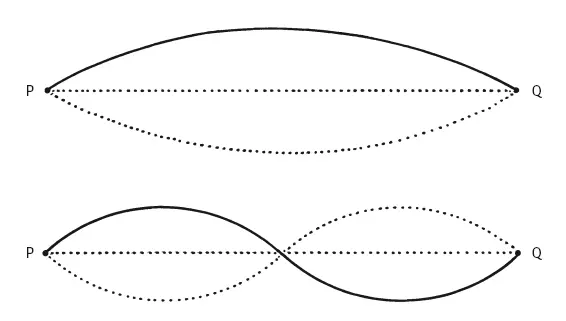
Струны, колеблющиеся в соотношении 2:i. Их колебания сходятся в одной точке (то есть приходят к согласию) после каждой второй пульсации (то есть отступления от оси) более короткой струны

Теория Бенедетти выглядела так: поскольку октава образуется из соотношения двух колеблющихся струн 2:1, каждое второе колебание, производимое более высокой струной, будет совпадать с колебанием, производимым более низкой струной. Когда пропорции, образующие различные созвучия, усложняются, это приводит к тому, что подобное совпадение колебаний происходит все реже и реже – поэтому они звучат менее консонантно. А значит, несмотря на утверждения Пифагора и Царлино, не существует единого набора гармоничных соотношений: диссонансы возникают нерегулярно.

Галилео Галилей развил эту мысль. Возьмем две струны, колеблющиеся в соотношении 3:2, объяснял он. Их пульсация начнется одновременно, затем произойдет колебание верхней струны, дальше нижней, потом опять верхней, и, наконец, цикл замкнется очередным одновременным колебанием обеих струн (этот ритмический рисунок легко изобразить, постукивая по столешнице двумя руками – одной в трехдольном ритме, другой в двудольном). По мере усложнения музыкальных интервалов рисунок будет становиться все более хаотичным, а звучание – неприятным, подвергающим “барабанную перепонку постоянной пытке, сгибающим ее одновременно в противоположных направлениях, посылающим ей противоположные сигналы”, другими словами – диссонантным.

В соответствии с семейной традицией Галилеев эстетические приципы, которые Галилео вывел из своей теории, были использованы для того, чтобы вбить еще один кол в и без того не слишком устойчивое здание системы Царлино. Октава, провозгласил он, вовсе не является чудесным созвучием – напротив, это очень пресное сочетание нот, поскольку ритмический рисунок 2:1 чрезвычайно скучен. То ли дело квинта, которая во всей своей сложности дает на выходе интересную комбинацию “сладости и остроты”!

Так или иначе, и эта теория консонанса не обошлась без существенных изъянов. Если принять ее за основу, то получится, что две струны будут звучать гармонично, только если их вибрации начинаются в одно и то же мгновение – ведь иначе их чередующиеся колебания никогда не сойдутся в одной точке! Но практика показывает, что это вовсе не так (и именно поэтому Ньютон с ходу отверг теорию Галилея). Есть и еще одна неувязка: пульсации струн, образующие сложное соотношение квинты в равномерно-темперированном строе, не сойдутся вновь, даже будучи изначально “запущены” одновременно. При этом равномерная квинта, разумеется, звучит более стройно, чем, скажем, полутон (например, сочетание нот ми и фа), в котором вибрации двух струн сходятся воедино на каждом пятнадцатом колебании. Словом, эта гипотеза была попросту неверна.