Алексей Жабров - Почему и как летает самолет [Изд. 2-е]

Когда самолет стоит на земле и силовая установка работает, то лопасти винта имеют только одну скорость — окружную (рис. 17, а). Значит, воздух набегает на лопасть по направлению стрелки В, показанной в плоскости вращения винта. Угол между этой стрелкой и хордой профиля лопасти будет, очевидно, углом атаки. Как видим, при неподвижном воздухе он равен углу установки лопасти к плоскости вращения. Иначе получается в полете, когда, кроме вращательного движения, винт движется еще и вперед (вместе с самолетом).

В полете эти движения складываются, и в результате лопасть движется по винтовой линии (рис. 17, б). Поэтому воздух набегает на лопасть по направлению стрелки В1 , и угол между ней и хордой профиля будет углом атаки. Вы видите, что угол атаки стал меньше угла установки. И чем больше будет скорость полета, тем меньше станут углы атаки лопастей, а поэтому тем меньше станет и сила тяги (при неизменном числе оборотов винта).

Этот недостаток в особенности присущ простому винту, у которого угол установки лопастей, а тем самым и шаг винта, нельзя изменять в полете (простой винт имеет и другие недостатки). Гораздо более совершенен винт изменяемого шага (рис. 18).

Рис. 18. Трехлопастный воздушный винт изменяемого шага на пассажирском самолете.

Такой винт благодаря особому устройству втулки без участия летчика изменяет свой шаг. Когда летчик уменьшает скорость полета, шаг винта тотчас же уменьшается, когда же летчик увеличивает скорость, винт увеличивает шаг.

В современной авиации применяются почти исключительно винты изменяемого шага.

Высоко в небе летит пассажирский самолет (рис. 19).

Рис. 19. Пассажирский 27-местный самолет ИЛ-12 конструкции С. В. Ильюшина в горизонтальном полете.

Большие крылья легко несут воздушный корабль, а мощный гул винтов свидетельствует о напряженной работе двигателей. Самолет летит горизонтально, прямолинейно и равномерно…

Под действием каких сил происходит такой полет?

Из первого закона механики, открытого великим английским ученым Исааком Ньютоном (1643–1727), следует, что прямолинейное равномерное движение происходит без действия каких-либо сил — по инерции [12] Всякое тело сохраняет свое состояние покоя или прямолинейного равномерного движения до тех пор, пока какая-нибудь сила не выведет его из этого состояния (первый закон Ньютона, называемый законом инерции). . На первый взгляд это кажется совершенно непонятным, так как из жизни мы знаем, что без силы тяги невозможно осуществить прямолинейное равномерное движение. Но дело в том, что сила тяги нужна только для того, чтобы все время преодолевать тормозящую силу, от которой мы не можем избавиться. Если бы ее не было, то тело, раз получив движение, двигалось бы вечно — по инерции.

Приведем простой пример.

По реке движется моторная лодка с постоянной скоростью. Сила тяги гребного винта, преодолевая силу сопротивления воды и силу сопротивления воздуха, должна быть равна их сумме, иначе равномерного движения не получится: если сила тяги будет больше тормозящих сил, движение будет ускоренным, если сила тяги станет меньше их, движение замедлится. Таким образом, для прямолинейного равномерного движения лодки необходимо, чтобы действующие на нее силы взаимно уравновешивались, то есть чтобы сумма их равнялась нулю. А ведь это и означает, что такое движение происходит без каких-либо сил — по инерции.

Следовательно, и для прямолинейного полета с постоянной скоростью (установившегося полета) тоже необходимо, чтобы действующие на самолет силы взаимно уравновешивались. Это справедливо как для горизонтального полета, так и для подъема и спуска.

Вот самолет летит горизонтально и прямолинейно (рис. 20) с постоянной скоростью при некотором угле атаки α .

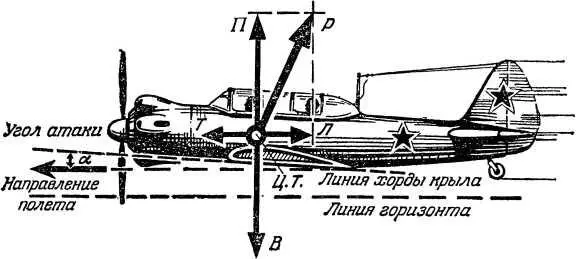
Рис. 20. Силы, действующие на самолет в установившемся горизонтальном полете. Подъемная сила П равна силе веса В, а сила тяги винта Т равна силе лобового сопротивления Л; Ц. Т. — центр тяжести.

На самолет действуют три главные силы: сила веса В сила тяги Т и полная аэродинамическая сила Р всего самолета, которую удобнее представить в виде ее слагаемых — подъемной силы П и силы лобового сопротивления Л.