Виктор Вайскопф - Наука и удивительное [Как человек понимает природу]

Теперь мы уже не можем получать любые частоты колебаний или любые длины волн. Действительно, можно возбудить только такие колебания, полуволна которых один, два или любое целое число раз укладывается в промежутке, разделяющем точки закрепления (рис. 25).

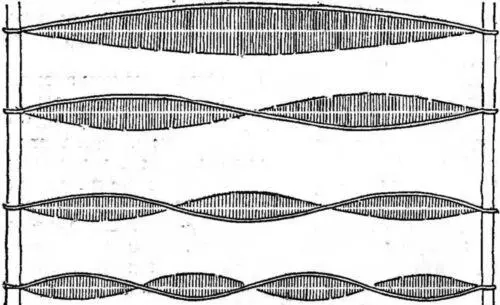
Рис. 25. Стоячие волны. Колебания струны, закрепленной в двух точках. Возникают только такие колебания, при которых между закрепленными точками укладываются только 1, 2, 3, 4 и т. д. полуволны. Горизонтальная прямая-положение струны в покое.

При постоянном натяжении струны определены не только формы колебаний, но и их частоты (числа колебаний в 1 сек ). Каждое из различных колебаний, которые можно возбудить в такой струне, имеет свою характерную частоту, так что струна может колебаться только с одной из этого ряда частот. Наименьшая частота, возбудить которую легче всего, отвечает полуволне, в точности укладывающейся один раз на расстоянии между точками закрепления. Ее и получает скрипач, приводя струну в движение смычком. Однако можно возбудить и колебания высших порядков, так называемые флажолетные тона, при которых в струне укладываются две или большее число полуволн.

Даже когда звучит основной тон, движение струны не отвечает только колебаниям низшего типа. Истинное движение струны является комбинацией различных разрешенных типов движения. В действительности обычный музыкальный тон скрипки содержит известное количество высших частот, называемых гармониками. Их присутствие важно для красоты звука. Разница между игрой Пабло Казальса и игрой заурядного виолончелиста заключается в различной примеси высших частот. Но, какова бы ни была эта комбинация, в нее могут входить только те частоты, которые содержатся в наборе разрешенных комбинаций.

Данные, полученные нами при изучении струны, справедливы для волн всех видов. Если волны распространяются в ограниченном пространстве, мы видим систему волн определенных типов с рядом частот, характерных для данной системы. На этом основано большинство музыкальных инструментов. В струнных инструментах используются ряды дискретных частот, характерных для колебаний данной струны. В духовых инструментах используются определенные частоты воздушных волн, заключенных в трубе, будь то тромбон или органная труба.

Другой интересный пример таких волн легко увидеть при наблюдении волн на воде, распространяющихся в ограниченном пространстве, например в стакане. Поразительную картину можно обнаружить, наблюдая за поверхностью воды в стакане. В летящем винтовом самолете, когда частота колебаний мотора становится равной одной из возможных частот колебаний воды в стакане, становится заметной специфическая картина поверхностных волн. При изменении частоты дрожания мотора или при изменении количества воды в резонанс с дрожанием приходят другие колебания. Бы увидите колебания с характерными частотами, которые связаны с определенными волновыми картинами.

Вполне возможно рассчитать форму этих картин и предсказать, при каких частотах следует ожидать их появления. Для этого нужно только знать форму и размер стакана и свойства волн на поверхности воды.

Электронные волны и квантовые состояния . Вернемся теперь к электронным волнам. Как можно ограничить в пространстве электронные волны и наблюдать явления, подобные описанным? В любой ситуации, ограничивающей движения электронов, будут ограничены и электронные волны. Такая ситуация возникает, например, тогда, когда электрон находится близко от атомного ядра. Положительный заряд ядра притягивает электрон и мешает ему покинуть область, непосредственно примыкающую к ядру; движение электрона ограничено пространством, близким к ядру. Как это скажется на электронных волнах? Такой вопрос, поставил Эрвин Шредингер в 1926 г., и он же ответил на него.

Ему удалось рассчитать форму и частоты характеристических волновых картин, которые получаются, когда электрон привязан к ядру. Если известна связь между длиной электронной волны и скоростью электрона, это сводится к простой задаче динамики стоячих волн. Результат дает ряд отдельных колебаний, из которых каждое отвечает определенной волновой картине и определенной частоте. Волновая природа электрона сразу же «объясняет», почему электрон в атоме может обладать только определенными формами движения.