Richard Rhodes - The Making of the Atomic Bomb

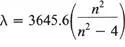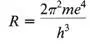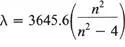
(the Greek letter λ , lambda, stands for the wavelength of the line; η takes the values 3, 4, 5 and so on for the various lines). Using his formula, Balmer was able to predict the wavelengths of lines to be expected for parts of the hydrogen spectrum not yet studied. They were found where he said they would be.

A Swedish spectroscopist, Johannes Rydberg, went Balmer one better and published in 1890 a general formula valid for a great many different line spectra. The Balmer formula then became a special case of the more general Rydberg equation, which was built around a number called the Rydberg constant. That number, subsequently derived by experiment and one of the most accurately known of all universal constants, takes the precise modern value of 109,677 cm −1.

Bohr would have known these formulae and numbers from undergraduate physics, especially since Christensen was an admirer of Rydberg and had thoroughly studied his work. But spectroscopy was far from Bohr’s field and he presumably had forgotten them. He sought out his old friend and classmate, Hans Hansen, a physicist and student of spectroscopy just returned from Göttingen. Hansen reviewed the regularity of line spectra with him. Bohr looked up the numbers. “As soon as I saw Balmer’s formula,” he said afterward, “the whole thing was immediately clear to me.” 280

What was immediately clear was the relationship between his orbiting electrons and the lines of spectral light. Bohr proposed that an electron bound to a nucleus normally occupies a stable, basic orbit called a ground state. Add energy to the atom—heat it, for example—and the electron responds by jumping to a higher orbit, one of the more energetic stationary states farther away from the nucleus. Add more energy and the electron continues jumping to higher orbits. Cease adding energy—leave the atom alone—and the electrons jump back to their ground states, like this:

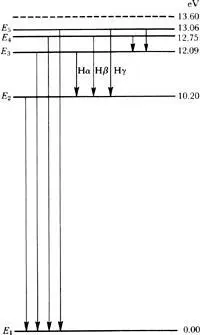
With each jump, each electron emits a photon of characteristic energy. The jumps, and so the photon energies, are limited by Planck’s constant. Subtract the value of a lower-energy stationary state W 2from the value of a higher energy stationary state W 1and you get exactly the energy of the light as hv. So here was the physical mechanism of Planck’s cavity radiation.

From this elegant simplification, W 1— W 2= hv , Bohr was able to derive the Balmer series. The lines of the Balmer series turn out to be exactly the energies of the photons that the hydrogen electron emits when it jumps down from orbit to orbit to its ground state.

Then, sensationally, with the simple formula

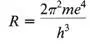
(where m is the mass of the electron, e the electron charge and h Planck’s constant—all fundamental numbers, not arbitrary numbers Bohr made up) Bohr produced Rydberg’s constant, calculating it within 7 percent of its experimentally measured value! “There is nothing in the world which impresses a physicist more,” an American physicist comments, “than a numerical agreement between experiment and theory, and I do not think that there can ever have been a numerical agreement more impressive than this one, as I can testify who remember its advent.” 281

“On the constitution of atoms and molecules” was seminally important to physics. Besides proposing a useful model of the atom, it demonstrated that events that take place on the atomic scale are quantized: that just as matter exists as atoms and particles in a state of essential graininess, so also does process. Process is discontinuous and the “granule” of process—of electron motions within the atom, for example—is Planck’s constant. The older mechanistic physics was therefore imprecise; though a good approximation that worked for large-scale events, it failed to account for atomic subtleties.

Bohr was happy to force this confrontation between the old physics and the new. He felt that it would be fruitful for physics. Because original work is inherently rebellious, his paper was not only an examination of the physical world but also a political document. It proposed, in a sense, to begin a reform movement in physics: to limit claims and clear up epistemological fallacies. Mechanistic physics had become authoritarian. It had outreached itself to claim universal application, to claim that the universe and everything in it is rigidly governed by mechanistic cause and effect. That was Haeckelism carried to a cold extreme. It stifled Niels Bohr as biological Haeckelism had stifled Christian Bohr and as a similar authoritarianism in philosophy and in bourgeois Christianity had stifled Søren Kierkegaard.

When Rutherford saw Bohr’s Part I paper, for example, he immediately found a problem. “There appears to me one grave difficulty in your hypothesis,” he wrote Bohr on March 20, “which I have no doubt you fully realise, namely, how does an electron decide what frequency it is going to vibrate at when it passes from one stationary state to the other? It seems to me that you would have to assume that the electron knows beforehand where it is going to stop.” 282Einstein showed in 1917 that the physical answer to Rutherford’s question is statistical—any frequency is possible, and the ones that turn up happen to have the best odds. But Bohr answered the question in a later lecture in more philosophical and even anthropomorphic terms: “Every change in the state of an atom should be regarded as an individual process, incapable of more detailed description, by which the atom goes over from one so-called stationary state to another…. We are here so far removed from a causal description that an atom in a stationary state may in general even be said to possess a free choice between various possible transitions.” 283The “catchwords” here, as Harald Høffding might say, are individual and free choice. Bohr means the changes of state within individual atoms are not predictable; the catchwords color that physical limitation with personal emotion.

In fact the 1913 paper was deeply important emotionally to Bohr. It is a remarkable example of how science works and of the sense of personal authentication that scientific discovery can bestow. Bohr’s emotional preoccupations sensitized him to see previously unperceived regularities in the natural world. The parallels between his early psychological concerns and his interpretation of atomic processes are uncanny, so much so that without the great predictive ability of the paper its assumptions would seem totally arbitrary.

Whether or not the will is free, for example, was a question that Bohr took seriously. To identify a kind of freedom of choice within the atom itself was a triumph for his carefully assembled structure of beliefs. The separate, distinct electron orbits that Bohr called stationary states recall Kierkegaard’s stages. They also recall Bohr’s attempt to redefine the problem of free will by invoking separate, distinct Riemann surfaces. And as Kierkegaard’s stages are discontinuous, negotiable only by leaps of faith, so do Bohr’s electrons leap discontinuously from orbit to orbit. Bohr insisted as one of the two “principal assumptions” of his paper that the electron’s whereabouts between orbits cannot be calculated or even visualized. 284Before and after are completely discontinuous. In that sense, each stationary state of the electron is complete and unique, and in that wholeness is stability. By contrast, the continuous process predicted by classical mechanics, which Bohr apparently associated with the licentiate’s endless ratiocination, tears the atom apart or spirals it into radiative collapse.