Obviously such was not the case. But what kept the energy in the cavity from running off infinitely into the far ultraviolet? Planck began his effort to find out in 1897 and pursued it for three hard years. Success came with a last-minute insight announced at a meeting of the Berlin Physical Society on October 19, 1900. Friends checked Planck’s new formula that very night against experimentally derived values. They reported its accuracy to him the next morning. “Later measurements, too,” Planck wrote proudly in 1947, at the end of his long life, “confirmed my radiation formula again and again—the finer the methods of measurement used, the more accurate the formula was found to be.” 277
Planck solved the radiation problem by proposing that the vibrating particles can only radiate at certain energies. The permitted energies would be determined by a new number—“a universal constant,” he says, “which I called h. Since it had the dimension of action (energy X time), I gave it the name, elementary quantum of action.” 278(Quantum is the neuter form of the Latin word quantus, meaning “how great.”) Only those limited and finite energies could appear which were whole-number multiples of hv: of the frequency ν times Planck’s h. Planck calculated h to be a very small number, close to the modern value of 6.63 × 10 −27erg-seconds. Universal h soon acquired its modern name: Planck’s constant.
Planck, a thoroughgoing conservative, had no taste for pursuing the radical consequences of his radiation formula. Someone else did: Albert Einstein. In a paper in 1905 that eventually won for him the Nobel Prize, Einstein connected Planck’s idea of limited, discontinuous energy levels to the problem of the photoelectric effect. Light shone on certain metals knocks electrons free; the effect is applied today in the solar panels that power spacecraft. But the energy of the electrons knocked free of the metal does not depend, as common sense would suggest, on the brightness of the light. It depends instead on the color of the light—on its frequency.
Einstein saw a quantum condition in this odd fact. He proposed the heretical possibility that light, which years of careful scientific experiment had demonstrated to travel in waves, actually traveled in small individual packets—particles—which he called “energy quanta.” Such photons (as they are called today), he wrote, have a distinctive energy hv and they transfer most of that energy to the electrons they strike on the surface of the metal. A brighter light thus releases more electrons but not more energetic electrons; the energy of the electrons released depends on hv and so on the frequency of the light. Thus Einstein advanced Planck’s quantum idea from the status of a convenient tool for calculation to that of a possible physical fact.
With these advances in understanding Bohr was able to confront the problem of the mechanical instability of Rutherford’s model of the atom. In July, at the time of the “little paper ready to show to Rutherford,” he already had his central idea. It was this: that since classical mechanics predicted that an atom like Rutherford’s, with a small, massive central nucleus surrounded by orbiting electrons, would be unstable, while in fact atoms are among the most stable of systems, classical mechanics was inadequate to describe such systems and would have to give way to a quantum approach. Planck had introduced quantum principles to save the laws of thermodynamics; Einstein had extended the quantum idea to light; Bohr now proposed to lodge quantum principles within the atom itself.
Through the autumn and early winter, back in Denmark, Bohr pursued the consequences of his idea. The difficulty with Rutherford’s atom was that nothing about its design justified its stability. If it happened to be an atom with several electrons, it would fly apart. Even if it were a hydrogen atom with only one (mechanically stable) electron, classical theory predicted that the electron would radiate light as it changed direction in its orbit around the nucleus and therefore, the system losing energy, would spiral into the nucleus and crash. The Rutherford atom, from the point of view of Newtonian mechanics—as a miniature solar system—ought to be impossibly large or impossibly small.
Bohr therefore proposed that there must be what he called “stationary states” in the atom: orbits the electrons could occupy without instability, without radiating light, without spiraling in and crashing. He worked the numbers of this model and found they agreed very well with all sorts of experimental values. Then at least he had a plausible model, one that explained in particular some of the phenomena of chemistry. But it was apparently arbitrary; it was not more obviously a real picture of the atom than other useful models such as J. J. Thomson’s plum pudding.
Help came then from an unlikely quarter. A professor of mathematics at King’s College, London, J. W. Nicholson, whom Bohr had met and thought a fool, published a series of papers proposing a quantized Saturnian model of the atom to explain the unusual spectrum of the corona of the sun. The papers were published in June in an astronomy journal; Bohr didn’t see them until December. He was quickly able to identify the inadequacies of Nicholson’s model, but not before he felt the challenge of other researchers breathing down his neck—and not without noticing Nicholson’s excursion into the jungle of spectral lines.
Oriented toward chemistry, communicating back and forth with George de Hevesy, Bohr had not thought of looking at spectroscopy for evidence to support his model of the atom. “The spectra was a very difficult problem,” he said in his last interview. “…One thought that this is marvelous, but it is not possible to make progress there. Just as if you have the wing of a butterfly, then certainly it is very regular with the colors and so on, but nobody thought that one could get the basis of biology from the coloring of the wing of a butterfly.” 279
Taking Nicholson’s hint, Bohr now turned to the wings of the spectral butterfly.
Spectroscopy was a well-developed field in 1912. The eighteenth-century Scottish physicist Thomas Melvill had first productively explored it. He mixed chemical salts with alcohol, lit the mixtures and studied the resulting light through a prism. Each different chemical produced characteristic patches of color. That suggested the possibility of using spectra for chemical analysis, to identify unknown substances. The prism spectroscope, invented in 1859, advanced the science. It used a narrow slit set in front of a prism to limit the patches of light to similarly narrow lines; these could be directed onto a ruled scale (and later onto strips of photographic film) to measure their spacing and calculate their wavelengths. Such characteristic patterns of lines came to be called line spectra. Every element had its own unique line spectrum. Helium was discovered in the chromosphere of the sun in 1868 as a series of unusual spectral lines twenty-three years before it was discovered mixed into uranium ore on earth. The line spectra had their uses.
But no one understood what produced the lines. At best, mathematicians and spectroscopists who liked to play with wavelength numbers were able to find beautiful harmonic regularities among sets of spectral lines. Johann Balmer, a nineteenth-century Swiss mathematical physicist, identified in 1885 one of the most basic harmonies, a formula for calculating the wavelengths of the spectral lines of hydrogen. These, collectively called the Balmer series, look like this:
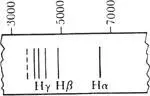
Balmer series
It is not necessary to understand mathematics to appreciate the simplicity of the formula Balmer derived that predicts a line’s location on the spectral band to an accuracy of within one part in a thousand, a formula that has only one arbitrary number:
Читать дальше













