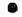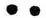Владимир Кузьмищев - Тайна жрецов майя

11 =

12 =

13 =

14=

15=

16=

17 =

18 =

19 =

Однако на этом похождения раковины-нуля не кончались. Раковина все же стала появляться и без точки, располагаясь на разных полках цифровой этажерки майя. Это означало, что настоящее число было образовано без участия единиц той полки, на которой в данном случае находилась раковина. Она говорила, что единиц этой полки (на которой она расположилась) попросту нет, как нет, например, десятков, сотен или тысяч в числе, записанном арабскими цифрами, если на отведенном для них месте стоят нули.

Но коль скоро в числе наличествовала хотя бы одна-единственная единица любой из полок, довольно сложный рисунок раковины-нуля сразу же исчезал с нее. Покажем это условно на простейшем примере:

(20) +

(1) =

, что соответствует числу 21 в нашем представлении.

Действительно, если нижняя точка находится на нижней полке, то это обозначает наличие одной единицы первой позиции, или, попросту говоря, «единицу», но уже не как абстрактный цифровой знак, а как конкретное число. Верхняя же полка указывает на наличие одной единицы второго порядка, каковой является двадцатка в двадцатеричной системе. Следовательно, перед нами двузначное число 21, образованное в полном соответствии со строгими законами позиционного принципа, но только расположенное не горизонтально, как мы привыкли, а вертикально. Проверим свой вывод простейшим арифметическим действием — сложением:

1 «единица» + 1 «двадцатка» = 21.

Чтобы окончательно усвоить урок математики майя, рассмотрим написание нескольких двузначных чисел майя; они наглядно продемонстрируют технику применения ими позиционного принципа, условно названного нами «числовой этажеркой майя»:

= 20

+ = 21;

= 1

= 20

+ = 22;

= 2

= 40

+ = 41;

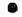
= 1

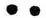
= 40

+ = 45;

= 5

= 60

+ = 61;

= 1

= 80

+ = 84;

= 4

= 100

+ =101;

= 1

= 120

+ = 126;

= 6

= 240

+ = 256;

= 16

= 340

+ = 359…

= 19

Здесь было бы вполне естественно написать «и так далее», однако это самое «и так далее» как раз и не получается…

В двадцатеричной системе счета древних майя есть исключение: стоит прибавить к числу «359» только одну-единственную единицу первого порядка, как это исключение немедленно вступает в силу. Суть его сводится к следующему: число 360 является начальным числом третьего порядка (!), и его место уже не на второй, а на третьей полке.

Но тогда выходит, что начальное число третьего порядка больше начального числа второго не в двадцать раз (20X20 = 400, а не 360!), а только в восемнадцать! Значит принцип двадцатеричности нарушен! Все верно. Дело обстоит именно так. Это и есть исключение.