Стивен Вайнберг - Объясняя мир. Истоки современной науки

Самая простая волна имеет синусоидальную форму. Если мы сделаем мгновенный снимок такой волны, то увидим, что у нее отклонение колеблющейся величины от среднего значения обращается в ноль в некоторых точках на пути ее распространения. Если, начав с одной из них, мы будем двигаться от нее вперед в направлении распространения волны, то увидим, как отклонение от среднего плавно увеличивается, пока не сравняется с амплитудой волны, и затем плавно опускается до нуля. Если мы последуем дальше, то увидим, что отклонение падает до отрицательного значения амплитуды и вновь возвращается к нулю, а затем весь цикл повторяется снова и снова по мере того, как мы двигаемся дальше в прежнем направлении. Расстояние между двумя соседними точками в начале и в конце полного цикла называется длиной волны и обычно обозначается символом λ (лямбда). Для восприятия дальнейшего объяснения важно понять, что, поскольку мгновенный уровень возвращается к нулю не только в начале и конце цикла, но еще и в середине, расстояние между двумя соседними нулевыми точками равняется половине длины волны, λ/2. Это значит, что любые две мгновенные точки с нулевым уровнем волны должны быть отделены друг от друга целым количеством отрезков с длиной, равной половине длины волны.

В математике есть фундаментальная теорема (впервые сформулированная только в первой половине XIX в.), которая доказывает, что практически любое возмущение (точнее, любое возмущение, достаточно гладко изменяющееся вдоль линии распространения волны) можно представить как результат сложения синусоидальных волн с разными длинами (это называется гармоническим анализом, или «фурье-анализом»).

Каждая синусоидальная волна предполагает не только изменение некой величины в пространстве, но и ее колебания. Если волна распространяется со скоростью v , то за время t она проходит расстояние vt . Тогда мимо фиксированной точки за время t проследует vt /λ интервалов, равных длине волны. Это значит, что в любой точке за одну секунду количество циклов, в течение каждого из которых и сама колеблющаяся величина, и скорость ее изменения вновь возвращаются к исходным значениям, равно v/λ. Эта величина называется частотой колебаний, и ее принято обозначать греческой буквой ν (ню), то есть ν = v/λ. Скорость распространения возмущения колеблющейся струны равна постоянной величине, если масса и натяжение струны практически не зависит от длины волны, и амплитуда колебаний определяется только массой струны и силой ее натяжения. Поэтому для таких волн (так же как и для световых волн) частота просто обратно пропорциональна длине волны.

Теперь рассмотрим струну какого-нибудь музыкального инструмента. Пусть ее длина равна L . Амплитуда колебаний должна равняться нулю на обоих концах струны, в точках ее крепления. Это условие ограничивает возможные длины волн синусоидальных составляющих, на которые раскладывается любое частное колебания струны. Как мы отметили, расстояние между любыми точками синусоидальной волны, где амплитуда колебания равна нулю, должно быть кратно половине длины волны. Значит, зафиксированная на обоих концах струна должна содержать целое число N таких интервалов в половину длины волны, то есть L = Nλ /2. Это означает, что в струне возможны только волны, длины которых выражаются формулой λ = 2L/N , где N = 1, 2, 3, и т. д. Соответственно, все возможные частоты можно найти по формуле [28]:

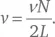
Самая низкая частота для случая, когда N = 1, равна v /2 L . Все прочие частоты, соответствующие N = 2, 3, 4 и т. д., называются обертонами. Например, самая низкая частота для струны ноты до первой октавы («среднее до») – 261,63 колебаний в секунду, но еще она же вибрирует с частотой 523,26 колебаний в секунду, 784,89 колебаний в секунду и т. д. Интенсивность различных обертонов определяет качество звучания разных музыкальных инструментов.

Теперь допустим, что вибрировать заставили две струны с длинами L 1и L 2, которые в остальном абсолютно одинаковы – в частности, скорость v распространения возмущения в обеих одинакова. За время t форма колебаний первой и второй струн на самых низких частотах для обеих пройдет через n 1= ν 1 t = vt /2 L 1и n 2= ν 2 t = vt /2 L 2циклов или частичных циклов, соответственно. Их соотношение равняется:

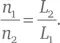
Таким образом, для того, чтобы частоты самого низкого из возможных для каждой из струн звуков относились как целые числа, величина L 2/ L 1 должна выражаться простой целочисленной дробью, то есть рациональным числом (в этом случае и для каждого обертона частоты будут удовлетворять тому же условию). Звуки обеих струн в этом случае сольются, как если бы щипнули одну струну, а не две. По всей видимости, именно поэтому мы воспринимаем получившееся созвучие как консонанс.