Jose Santonja - Физика учит новый язык. Лейбниц. Анализ бесконечно малых.

В греческой математике не было создано общих методов для решения различных задач. Кроме того, после подчинения геометрии математической строгости доказательства стали каждый раз все более сложными. Это мешало двигаться дальше в развитии вычислений.

Этот метод обязан своим существованием греческому математику Евдоксу Книдскому (ок. 390-337 до н.э.). Он состоит в приближении неизвестной площади, которую нужно вычислить, к большей или меньшей площади. Метод основывается на принципе, который упоминается в "Началах" Евклида:

"Если при данных двух неравных величинах из наибольшей величины вычесть величину, большую ее половины, а из остатка — другую величину, большую ее половины, и последовательно повторять процесс, в итоге останется величина, меньшая наименьшей из заданных величин".

Попробуем найти площадь круга (рисунок 1). Для этого впишем в него квадрат (площадью, большей половины круга) и вычтем его площадь из круга. На сторонах квадрата построим равнобедренные треугольники, вписанные в сегменты круга, а затем вычтем площадь данных треугольников. Повторяя последнюю операцию нужное количество раз, мы последовательно подходим к площади круга сколь угодно близко.

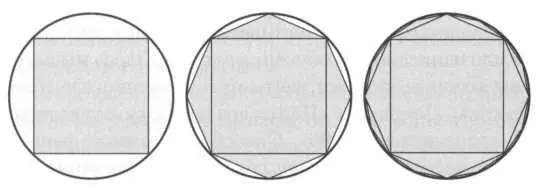
РИС. 1

На рисунках видно, что каждый раз происходит вписывание в круг многоугольников с большим числом сторон, площадь которых каждый раз все больше приближается к искомой площади круга. Такие же рассуждения можно применить к описанному квадрату (рисунок 2).

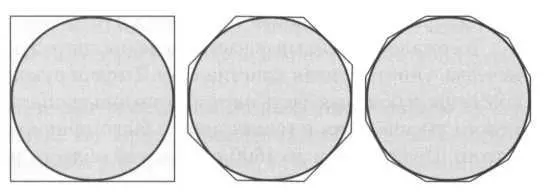
РИС. 2

Изначально развитие греческой арифметики было обусловлено потребностями геометрии, поскольку математики сводили ее к вычислению геометрических или тригонометрических величин. Позже арифметика и алгебра разделились и начали развиваться как независимые дисциплины. Математики христианской эпохи, такие как Герои Александрийский (I в.), Никомах Герасский (II в.) и Диофант Александрийский (III в.), развивали арифметику и алгебру без оглядки на потребности геометрии. Никомах, следовавший пифагорейской традиции и написавший "Введение в арифметику", считал, что его труд имел такое же значение для арифметики, как "Начала" Евклида — для геометрии.

Древнегреческая алгебра добилась огромных успехов благодаря Диофанту. Его "Арифметика" состоит из серии задач с решениями и необходимыми разъяснениями. Это сочинение было написано для обучения алгебре. Здесь мы встречаем задачи, которые, кажется, взяты из современного учебника средней школы. Например: "Найти два числа, сумма которых равна 20, а произведение — 96". Способ, которым ее решает Диофант, если использовать нашу современную терминологию, выглядит следующим образом. Сумма равна 20, а произведение 96; пусть 2х есть разность между наибольшим и наименьшим числом; следовательно, оба числа равны 10 + х и 10 - х, а их произведение (10+х)(10-х) = 100 - х 2= 96, х 2= 4. Следовательно, х = 2, поскольку ученые Древней Греции не учитывали отрицательных решений. Искомые числа — 12 и 8.

К сожалению, большая часть наследия греческой культуры исчезла, уничтоженная христианами. Тысячи рукописей были сожжены, и большая часть научного знания пропала. В течение целого тысячелетия в геометрию не было привнесено ничего нового. Практически до 1600 года в этой области не происходило никакого развития.

В середине XVI века по Европе начали распространяться латинские переводы сохраненных арабскими учеными основных греческих текстов, которые были с энтузиазмом приняты математиками того времени. Началось тщательное изучение решений задач и доказательств, найденных древнегреческими учеными. Восхищение математиков XVI и XVII веков знаниями греков было бесспорным.

Геометрия в течение тысячелетия стояла на месте, но алгебра немного развивалась, что сделало возможным создание математического анализа. Алгебра все еще была тесно связана с геометрией. Математик Мухаммад ибн Муса Аль-Хорезми (780- 850) работал в Багдаде. От его имени происходит слово алгоритм. Также благодаря ему появилось слово алгебра, поэтому многие авторы считают Аль-Хорезми отцом алгебры. Однако метод, которым он пользовался для решения своих уравнений, оставался в основном геометрическим.