Брайан Кокс - Почему Е=mc²? И почему это должно нас волновать

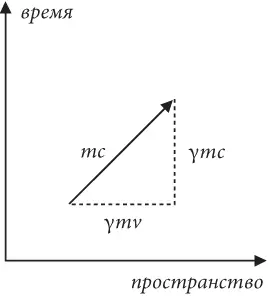
Рис. 13

Следует помнить, что импульс интересует нас только потому, что он сохраняется. Поэтому мы искали новый четырехмерный импульс, который будет сохраняться в пространстве-времени. Мы можем представить себе совокупность векторов импульса, указывающих в разных направлениях. Они могут отображать, например, импульсы определенного количества частиц, которые должны вот-вот столкнуться. После столкновения образуется новая совокупность векторов импульса, указывающих в других направлениях. Однако закон сохранения импульса гласит, что общая сумма всех новых стрелок должна в точности соответствовать сумме исходных. Это, в свою очередь, означает, что должна сохраняться также общая сумма частей всех стрелок, указывающих в направлении пространства, так же как и сумма частей, указывающих в направлении времени. Таким образом, если мы подсчитаем значения γ mv для каждой частицы, то общая сумма этих значений до столкновения должна быть такой же, как и общая сумма после него. То же самое происходит и с частями вектора импульса, указывающими в направлении времени, только в этом случае сохраняется общая сумма значений γ mc . Похоже, у нас есть два новых закона физики: γ mv и γ mc – это сохраняющиеся величины. Но чему они соответствуют? На первый взгляд во всем этом нет ничего особенного. Если скорость достаточно низкая, то значение γ очень близко к единице, а γ mv превращается просто в mv . Таким образом, в итоге все тот же закон сохранения импульса. Это обнадеживает, поскольку мы рассчитывали, что нам удастся прийти к выводам, которые признали бы физики викторианской эпохи. Безусловно, Брюнель и другие великие инженеры XIX столетия прекрасно обходились без пространства-времени, поэтому наше новое определение импульса должно давать почти те же ответы, что и во времена промышленной революции, – при условии, что объекты перемещаются со скоростью, далекой от скорости света. В конце концов, Клифтонский подвесной мост не упал после того, как Эйнштейн сформулировал теорию относительности.

Что мы можем сказать о сохранении γ mc ? Поскольку c – это универсальная константа, значение которой всегда одинаково, закон сохранения γ mc равносилен утверждению, что масса сохраняется. Этот вывод не стал для нас большой неожиданностью, поскольку согласуется с интуицией, хотя довольно интересно, что он появился как будто ниоткуда. Например, можно утверждать, что после сгорания угля в печи масса пепла (плюс масса вещества, вылетевшего через дымоход) должна быть равна массе угля до его сжигания. Тот факт, что значение γ не равно в точности единице, кажется несущественным, и у нас может возникнуть соблазн двигаться дальше, удовлетворившись тем, что мы и так уже многого добились. Мы определили импульс таким образом, что он представляет собой значимую величину в пространстве-времени, благодаря чему внесли коррективы (в большинстве случаев незначительные) в определение импульса, принятое в XIX столетии, и в то же время вывели закон сохранения массы. На что еще мы могли рассчитывать?

Нам понадобилось достаточно много времени, чтобы добраться до этого момента, но нас все же ждет неожиданный финал этого повествования. Мы более внимательно проанализируем ту часть вектора импульса, который указывает направление во времени, а сделав это, чудесным образом выведем самую знаменитую формулу Эйнштейна. Мы с вами проделали большой путь, и вы узнали многое из того, что должен знать профессиональный физик о четырехмерных векторах и пространстве Минковского. Теперь мы готовы к кульминации.

Мы установили, что значение γ mc должно сохраняться. Теперь нам необходимо объяснить, что именно это означает. Если вы представите себе игру в релятивистский бильярд, то в ней каждый шар имеет свое значение γ mc . Сложите вместе все эти значения – и какой бы ни была общая сумма, она останется неизменной. А теперь давайте поиграем в игру, которая поначалу покажется бессмысленной. Если значение γ mc сохраняется, то сохраняется и значение γ mc ² – просто потому, что c – это константа. Вскоре вам станет понятно, зачем мы так поступили. В то же время значение γ не равно в точности единице, и в случае малых скоростей его можно аппроксимировать посредством формулы γ = 1 + v ² ÷ 2 c ². С помощью калькулятора вы можете проверить самостоятельно, что эта формула работает достаточно хорошо для скоростей, которые можно считать малыми по сравнению с с (то есть она дает практически те же значения, что и точная формула γ = 1 ÷ √(1 − v ²/ с ²). Если у вас под рукой нет калькулятора, надеемся, представленная ниже таблица вас убедит. Обратите внимание, что приближенная формула (которая дает значения, представленные в третьем столбце) на самом деле очень точна даже в случае скоростей, составляющих десять процентов от скорости света ( v / c = 0,1), что представляет собой недостижимую в обычных условиях скорость 30 миллионов метров в секунду.