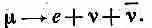
При этом распаде оказывается, что (по крайней мере при высоких энергиях) электроны испускаются преимущественно в направлении, противоположном направлению спина мюона.
Допустим затем, что имеется экспериментальное устройство (фиг. 5.9): поляризованные мюоны входят слева и в блоке вещества А останавливаются, а чуть позже распадаются.
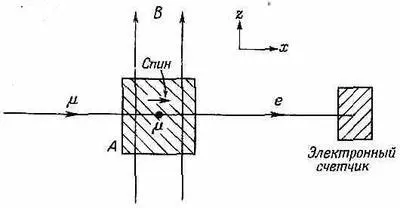
Фиг. . 5.9. Опыт с распадом мюона.
Испускаемые электроны выходят, вообще говоря, во всех мыслимых направлениях. Представим, однако, что все мюоны будут входить в тормозящий блок А так, что их спины будут повернуты в направлении х. Без магнитного поля там наблюдалось бы какое-то угловое распределение направлений распада; мы же хотим знать, как изменилось бы это распределение при наличии магнитного поля. Можно ожидать, что оно как-то будет меняться со временем. То, что получится, можно узнать, спросив, какой будет в каждый момент амплитуда того, что мюон обнаружится в состоянии (+ x ).
Эту задачу можно сформулировать следующим образом: пусть известно, что в момент t=0 спин мюона направлен по + х ; какова амплитуда того, что в момент т он окажется в том же состоянии? И хотя мы не знаем правил поведения частицы со спином 1/ 2в магнитном поле, перпендикулярном к спину, но зато мы знаем, что бывает с состояниями, когда спины направлены вверх или вниз по полю,— тогда их амплитуды умножаются на выражение (5.34). Наша процедура тогда будет состоять в том, чтобы выбрать представление, в котором базисные состояния — это направления спином вверх или спином вниз относительно z (относительно направления поля). И любой вопрос тогда сможет быть выражен через амплитуды этих состояний.
Пусть |y(t)> представляет состояние мюона. Когда он входит в блок А, его состояние есть |y (0)>, а мы. хотим знать |y (t)> в более позднее время t. Если два базисных состояния обозначить (+z) и (-z), то нам известны амплитуды <+z|y (0)> и <-z|y (0)> — они известны потому, что мы знаем, что |y (0)> представляет собой состояние со спином в направлении (+ x ). Из предыдущей главы следует, что эти амплитуды равны
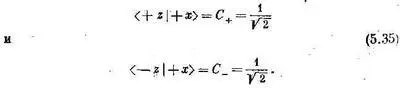
Они оказываются одинаковыми. Раз они относятся к положению при t=0, обозначим их С +(0) и С -(0).
Далее, мы знаем, что из этих двух амплитуд получится со временем. Из (5.34) следует
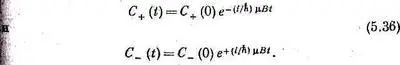
Но если нам известны C + (t) и C - (t), то у нас есть все, чтобы знать условия в момент t. Надо преодолеть только еще одно затруднение: нужна-то нам вероятность того, что спин (в момент t )окажется направленным по + х. Но наши общие правила учитывают и эту задачу. Мы пишем, что амплитуда пребывания в состоянии (+x) в момент t [обозначим ее A + ( t )]есть
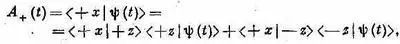
или
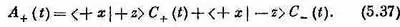
Опять пользуясь результатом последней главы (или лучше равенством
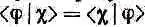 * из гл. 3), мы пишем
* из гл. 3), мы пишем
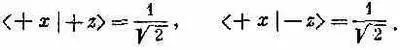
Итак, в (5.37) все известно. Мы получаем
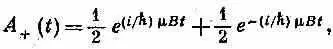
или
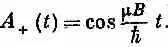
Поразительно простой результат! Заметьте: ответ согласуется с тем, что ожидалось при t= 0 . Мы получаем А + (0) = 1 , и это вполне правильно, потому что сперва и было предположено, что при t =0 мюон был в состоянии (+ x ).
Вероятность Р + того, что мюон окажется в состоянии (+х) в момент t, есть (А +) 2, т. е.
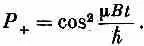
Вероятность колеблется от нуля до единицы, как показано на фиг. 5.10.
Читать дальше


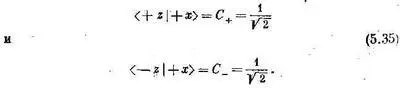
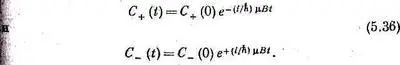
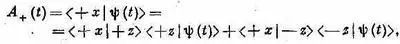
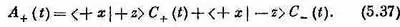
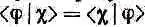 * из гл. 3), мы пишем
* из гл. 3), мы пишем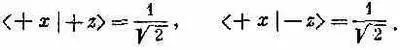
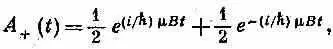
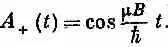
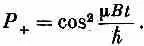



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


