|< > | 2 dS.
Сперва предположим, что частицы все различимы, тогда вероятность того, что n частиц будут одновременно зарегистрированы в n разных элементах поверхности, будет равна
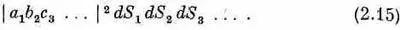
Опять примем, что амплитуды не зависят от того, где в счетчике расположен элемент dS (он считается малым), и обозначим их .просто а , b , с , .... Вероятность (2.15) обратится в
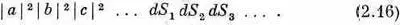
Прогоняя каждый элемент dS по всей поверхности D S счетчика, получаем, что Р n(разные) — вероятность одновременно зарегистрировать n разных частиц — равна
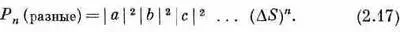
Это просто произведение вероятностей попаданий в счетчик каждой из частиц по отдельности. Все они действуют независимо — вероятность попасть для одной из них не зависит от того, сколько других туда попало.
Теперь предположим, что все эти частицы — идентичные бозе-частицы. Для каждой совокупности направлений 1, 2, 3, ... существует много неразличимых возможностей. Если бы, скажем, частиц было только три, появились бы следующие возможности:
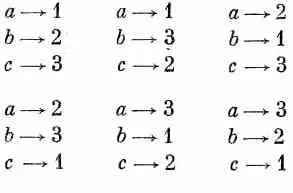
Возникает шесть различных комбинаций. А если частиц n, то будет n !разных, хотя и не отличимых друг от друга, комбинаций; их амплитуды положено складывать. Вероятность того, что n частиц будут зарегистрированы в n элементах поверхности, тогда будет равна
│ a 1 b 2 c 3 …+ a 1b 3c 2… + и т. д. +│ 2 dS 1 dS 2 dS 3... dS n . (2.18)
И снова мы предположим, что все направления столь близки друг к другу, что можно будет положить а 1=а 2= . . . . . . =а n = а и то же сделать с b, с, . . . ; вероятность (2.18) обратится в
|n ! abc ... | 2 dS 1 dS 2 ... dS n . (2.19)
Когда каждый элемент dS прогоняют по площади D S счетчика, то всякое мыслимое произведение элементов поверхности считается n !раз; учтем это, разделив на n !, и получим
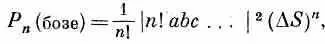
или
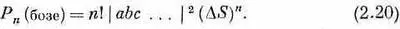
Сравнивая это с (2.17), видим, что вероятность совместного счета n бозе-частиц в n !раз больше, чем получилось бы в предположении, что все частицы различимы. Все это можно подытожить так:
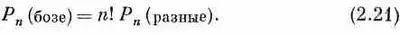
Итак, вероятность в случае бозе-частиц в n !раз больше, чем вы получили бы, считая, что частицы действовали независимо. Мы лучше поймем, что это значит, если спросим: чему равна вероятность того, что бозе-частица перейдет в некоторое состояние, в котором уже находятся n других частиц? Обозначим добавленную частицу буквой w. Если всего, включая w , имеется (n +1) частиц, то (2.20) обращается в
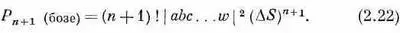
Это можно записать так:
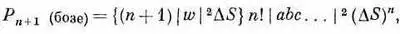
или
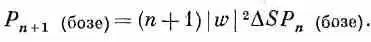
Этот результат можно истолковать следующим образом. Число |w| 2D S — это вероятность заполучить в счетчик частицу w, если никаких других частиц нет; Р n (бозе) — это шанс того, что там уже есть n других бозе-частиц. Значит, (2.23) говорит нам, что когда у нас уже есть n других идентичных друг другу бозе-частиц, то вероятность того, что еще одна частица придет в то же состояние, усиливается в (n +1) раз. Вероятность получить еще один бозон там, где уже есть их n штук, в ( n +1) раз больше той, какая была бы, если бы там раньше ничего не было. Наличие других частиц увеличивает вероятность заполучить еще одну.
Читать дальше

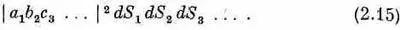
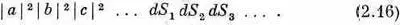
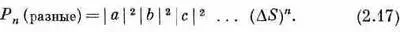
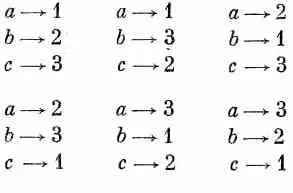
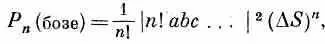
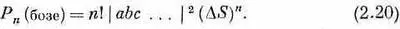
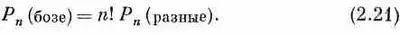
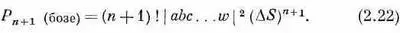
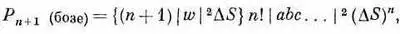
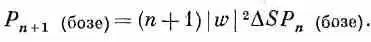



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


