w<<1/t
и
w<0. (32.49)
Давайте посмотрим, какие частоты соответствуют этому приближению для такого типичного металла, как медь. Для вычисления t воспользуемся уравнением (32.43), а для вычисления s/e 0— известными значениями s и e 0. Справочник дает нам такие данные:
s=5,76·10 7(ом·м) -1,
Атомный вес = 63,5 г,
Плотность = 8,9 г/см 3 ,
Число Авогадро=6,02·10 23.
Если мы предположим, что на каждый атом приходится по одному свободному электрону, то число электронов в кубическом метре будет равно
N=8,5·10 28м -3 .
Используя далее
q e=1,6·10 -1 9 кулон,
e 0=8,85·10 -12 ф/м,
m =9,11·10 -31 кг,
получаем
t=2,4·10 -14 сек,
1/t=4,l·10 13сек -1,
s/e 0= 6,5·10 18 сек -1 .
Таким образом, для частот, меньших чем приблизительно 10 12 гц, медь будет иметь описанное нами «низкочастотное» поведение. (Это будут волны с длиной, большей 0,3 мм, т. е. очень короткие радиоволны!)
Для таких волн глубина скин-слоя равна
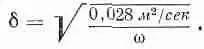
Для микроволн с частотой 10 000 Мгц (3-сантиметровые волны)
s=6,7·10 -4 см,
т. е. волны проникают на очень малое расстояние.
Теперь вы видите, почему при изучении полостей (и волноводов) нам нужно беспокоиться только о полях внутри полости, а не о волнах в металле или вне полости. Кроме того, мы видим, почему серебрение или золочение полости уменьшает потери в ней. Ведь потери происходят благодаря токам, которые ощутимы только в тонком слое, равном глубине скин-слоя.
Рассмотрим теперь показатель преломления в металле типа меди при высоких частотах. Для очень высоких частот сот много больше единицы, и уравнение (32.42) очень хорошо аппроксимируется следующим:

Для высокочастотных волн показатель преломления в металлах становится чисто вещественным и меньшим единицы! Это следует также из выражения (32.38), если пренебречь диссипативным членом с 7, что может быть сделано при очень больших значениях w. Выражение (32.38) дает при этом

что, разумеется, эквивалентно уравнению (32.50). Раньше нам
уже встречалась величина (Nq 2 e /e 0 m) 1/2 , которую мы назвали
плазменной частотой (см. гл. 7, § 3, вып. 5);
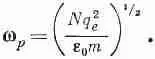
Таким образом, (32.50) или (32.51) можно переписать в виде
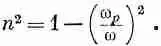
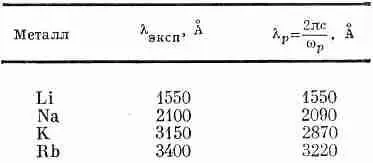
Эта плазменная частота является своего рода «критической». Для wрпоказатель преломления металла имеет мнимую часть и происходит поглощение волн, но при w>>w pпоказатель становится вещественным, а металл — прозрачным. Вы знаете, конечно, что металлы в достаточной мере прозрачны для рентгеновских лучей. Но некоторые металлы прозрачны даже для ультрафиолета. В табл. 32.3 мы приводим для некоторых металлов экспериментально наблюдаемые длины волн, при которых эти металлы начинают становиться прозрачными. Во второй колонке дана вычисленная критическая длина волны l p=2pc/w p. Учитывая, что экспериментальная длина волны определена не очень хорошо, согласие с теорией следует признать замечательным.
Таблица 32.3 · длины волн, при которых МЕТАЛЛ СТАНОВИТСЯ ПРОЗРАЧНЫМ
Вас может удивить, почему плазменная частота w рдолжна иметь отношение к распространению волн в металлах. Плазменная частота появилась у нас в гл. 7 (вып. 5) как собственная частота колебаний плотности свободных электронов. (Электрическое расталкивание группы электронов и их инерция приводят к колебаниям плотности.) Продольные волны плазмы резонируют при частоте w. Но сейчас мы говорим о поперечных волнах, и мы уже нашли, что при частотах, меньших w р , происходит их поглощение. (Это очень интересное и отнюдь не случайное совпадение.)
Читать дальше

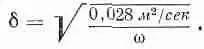


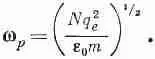
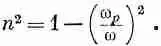




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
