Ричард Фейнман - 4a. Кинетика. Теплота. Звук

e ia e ib =(cos a+i sin a) (cos b+i sin b)

мы получаем cos a cos b- sinasinb плюс некоторая мнимая добавка. Сейчас, однако, нам нужна только вещественная часть. Таким образом,

cos (a+b) =cos a cos b- sin a sin b. (48.2)

Если теперь изменить знак величины b, то, поскольку коси­нус при этом не изменяет знака, а синус изменяет знак на обратный, мы получаем аналогичное выражение для косинуса разности

cos (a-b) =cos a cos b+ sin a sin b. (48.3)

После сложения этих двух уравнений произведение синусов сократится, и мы находим, что произведение двух косинусов равно половине косинуса суммы плюс половина косинуса разности

cos a cos b= 1 / 2 cos (а + b)+ 1 / 2 cos (a-b). (48.4)

Теперь можно обернуть это выражение и получить формулу для cosa+cosb, если просто положить a = а+b, a b= а- b, т. е. a = 1/ 2(a+b), a b= 1/ 2(a-b):

cosa+cosb=2cos 1/ 2(a+b) cos 1/ 2(a-b). (48.5)

Но вернемся к нашей проблеме. Сумма cosw 1t и cosw 2t равна

cosw 1t+cosw 2t=2cos 1/ 2(w 1+w 2)tcos 1/ 2(w 1-w 2)t. (48.6)

Пусть теперь частоты приблизительно одинаковы, так что 1/ 2(w 1+w 2) равна какой-то средней частоте, которая более или менее та же, что и каждая из них. Но разность w 1-w 2 гораздо меньше, чем w 1и w 2, поскольку мы предположили, что w 1и w 2приблизительно равны друг другу. Это означает, что результат сложения можно истолковать так, как будто есть косинусообразная волна с частотой, более или менее равной пер­воначальным, но что «размах» ее медленно меняется: он пульси­рует с частотой, равной 1 l 2 ( w 1 - w 2 )- Но та ли это частота, с которой мы слышим биения? Уравнение (48.6) говорит, что амплитуда ведет себя как cos 1/ 2(w 1-w 2), и это надо понимать так, что высокочастотные колебания заключены между двумя косинусоидами с противоположными знаками (пунктирная линия на фиг. 48.1). Хотя амплитуда действительно меняется с частотой 1/ 2(w 1-w 2), однако если речь идет об интенсивности волн, то мы должны представлять себе частоту в два раза боль­шую. Иначе говоря, модуляция амплитуды в смысле ее интен­сивности происходит с частотой w 1-w 2, хотя мы и умножаем на косинус половинной частоты.

Пренебрегая этими небольшими усложнениями, мы можем заключить, что если складывать две волны с частотами w 1и w 2, то получим волну с частотой, равной средней частоте 1/ 2(w 1+w 2), «сила» которой осциллирует с частотой w 1-w 2.

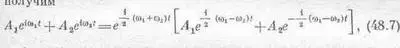
Если амплитуды двух волн различны, то можно, конечно, повторить все вычисления снова, умножив предварительно косинусы на различные амплитуды А 1 и А 2 и произведя массу всяких математических вычислений, перестроек и т. п. с исполь­зованием уравнений, подобных (48.2) — (48.5). Однако есть и другой, более легкий путь провести этот же анализ. Известно, например, что гораздо легче работать с экспонентами, чем с синусами и косинусами, поэтому можно представить A 1созw 1t как реальную часть экспоненты А 1 ехр (i w 1 t). Подобным же обра­зом вторая волна будет реальной частью A 2ехр(iw 2t). После сложения этих экспонент A 1exp (i w 1 t)+ A 2exp(iw 2t) и выделения в качестве множителя экспоненты со средней частотой мы получим

т. е. снова оказывается, что высокочастотная волна модули­руется малой частотой.

§ 2. Некоторые замечания о биениях и модуляции

Предположим теперь, что нас интересует интенсивность волны, описываемой уравнением (48.7). Чтобы найти ее, нужно взять квадрат абсолютной величины либо правой, либо левой части этого уравнения. Давайте возьмем левую часть. Интен­сивность при этом будет равна

I = A 2 1 +A 2 2 + 2A 1 A 2 cos( w l - w 2 )t. (48.8)

Видите, интенсивность возрастает и падает с частотой w 1-w 2, изменяясь в пределах между (А 1 + A 2 ) 2 и (А 1 -A 2 ) 2 . Если А 1 №А 2 , то минимальная интенсивность не равна нулю.

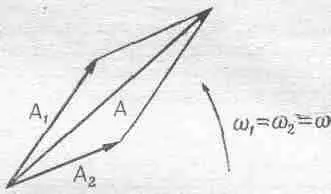
Те же результаты можно получить и другим путем—с по­мощью схем, подобных фиг. 48.2.

Фиг. 48.2. Результат сложения двух комплексных векторов с рав­ными частотами.

Изобразим одну из волн в виде вектора длиной A 1в комплексной плоскости, вращающе­гося с угловой скоростью w 1. Вторую волну изобразим другим вектором, длина которого A 2, а угловая скорость вращения w 2. Если эти частоты в точности равны между собой, то мы по­лучим вращающийся вектор, длина которого все время по­стоянна. Так что интенсивность в этом случае будет все время постоянной фиксированной величиной. Если, однако, частоты хоть немного отличаются одна от другой, то эти два вектора будут крутиться с различными скоростями.