Ричард Фейнман - 4a. Кинетика. Теплота. Звук

r 0 D x =r (( дc / д x) D x + D x), (47.6)

или

r 0=(r 0+r u) дc / д x+r 0+r u. (47.7)

Но в звуковой волне все изменения малы, так что r uмало, c мало и дc/дх тоже мало. Поэтому в уравнении, которое мы только что написали,

r u=-r 0( дc / д x)- r u( дc / д x), (47.8)

можно пренебречь r u (дc/дх) по сравнению с r 0 (дc/дх). Так мы приходим к соотношению, которое требовалось согласно свойству I:

(I) r u=-r 0 д c/ д x. (47.9)

Именно такой вид уравнения можно было ожидать из чисто физических соображений. Если смещение различно для разных х, плотность будет изменяться. Знак тоже правильный: если сме­щение c растет с ростом х, так что воздух расширяется, плотность должна уменьшаться.

Теперь нам нужно найти третье уравнение — уравнение движения, производимого избытком давления. Зная соотноше­ние между силой и давлением, можно получить уравнение дви­жения. Возьмем объем воздуха толщиной Dx и с единичной пло­щадью грани, перпендикулярной х, тогда масса воздуха в этом объеме есть r 0Dx, а ускорение воздуха есть д 2 c /дt 2 , так что масса, умноженная на ускорение для этого слоя, есть r 0Dx( д 2c/ д t 2). (Если Dx; мало, то безразлично, где брать ускорение — на краю слоя или где-нибудь посредине.) Сила, действующая на единич­ную площадку нашего слоя, перпендикулярную оси x, должна быть равна r 0Dx( д 2хc/ д t 2). В точке х мы имеем силу Р(х,t), дей­ствующую на единицу площади в направлении + х, а в точке x+Dx; возникает сила в обратном направлении, по величине равная Р(x;+ Dx, t) (фиг. 47.4):

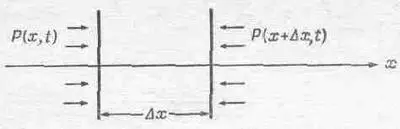
Фиг. 47.4. Результирующая сила в направлении оси х, возникающая за счет давления на единичную площадку, перпендикулярную к оси х, есть — (дР/дх)Dx.

Р(х, t)-P(x+ D x, t )=-( д P/ д x) Dx=( д P u/ д x) Dx. (47.10)

Мы учли, что Dx; мало и что только избыточное давление Р и меняется в зависимости от х. Итак, согласно свойству III мы получаем

(III) r 0= д 2c/ д t 2=- д P u/ д x. (47.11)

Теперь уже уравнений достаточно, чтобы увязать все вели­чины и привести к одной переменной, скажем х. Можно выразить Р u в (47.11) с помощью (47.4):

r 0 д 2c/ д t 2-c д r u/ д x (47.12)

а затем исключить r uс помощью (I). Тогда r 0сократится и у нас останется

д 2c/ д t 2=x д 2c/ д x 2. (47.13)

Обозначим с 2 s =x , тогда можно написать

Это и есть волновое уравнение, которое описывает распростра­нение звука в среде.

§ 4. Решения волнового уравнения

Посмотрим теперь, действительно ли волновое уравнение описывает основные свойства звуковых волн в среде. Прежде всего мы хотим вывести, что звуковое колебание, или возмуще­ние, движется с постоянной скоростью. Кроме того, нам нужно доказать, что два различных колебания могут свободно прохо­дить друг через друга, т. е. принцип суперпозиции. Мы хотим еще доказать, что звук может распространяться и вправо и влево. Все эти свойства должны содержаться в нашем одном урав­нении.

Раньше мы отмечали, что любое возмущение, имеющее вид плоской волны и движущееся с постоянной скоростью, записы­вается в виде f(x-vt). Посмотрим теперь, является ли f(x-vt) решением волнового уравнения. Вычисляя дc/дх, получаем производную функции dcldx=f'(x-vt). Дифференцируя еще раз, находим

Дифференцируя эту же функцию c по t, получаем значение — V, умноженное на производную, или д c /dt=-vf (x-vt); вторая производная по времени дает

Очевидно, что f(х-vt) удовлетворяет волновому уравнению, если v равно c s .

Таким образом, из законов механики мы получаем, что любое звуковое возмущение распространяется со скоростью c s и, кроме того,

тем самым мы связали скорость звуковых волн со свойствами среды.

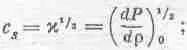
Легко увидеть, что звуковая волна может распространяться: и в направлении отрицательных х, т. е. звуковое возмущений вида c (х, t)=g(x+vt) также удовлетворяет волновому уравнению. Единственное отличие этой волны от той, которая распростра­нялась слева направо, заключается в знаке v, но знак д 2 c/dt 2 не зависит от выбора x+vt или х-vt, потому что в эту производ­ную входит только v 2. Отсюда следует, что решение уравнения описывает волны, бегущие в любом направлении со скоростью c s .