При достаточно большой энергии, когда Е/E 0 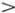 4, и даже при максимальном значении потенциальной энергии 4 sin 2(φ/2) (при φ = π потенциальная энергия равна 4) кинетическая энергия (φ') 2/ω 0 2не равна нулю, и маятник проскакивает верхнюю точку. Теперь он совершает не колебательное, а вращательное движение.
4, и даже при максимальном значении потенциальной энергии 4 sin 2(φ/2) (при φ = π потенциальная энергия равна 4) кинетическая энергия (φ') 2/ω 0 2не равна нулю, и маятник проскакивает верхнюю точку. Теперь он совершает не колебательное, а вращательное движение.
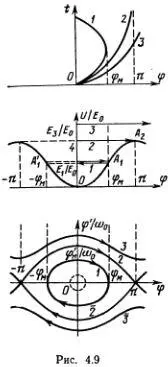
Это движение не равномерно, внизу скорость маятника максимальна, а в верхнем положении минимальна. На наших графиках это движение изображается кривыми 3. Если маятник вращается против часовой стрелки, значение угла φ неограниченно возрастает с ростом времени (фазовая траектория 3). Если он вращается по часовой стрелке, то значение угла неограниченно уменьшается (фазовая траектория 3).
Наиболее интересно для нас движение с энергией Е , в точности равной 4 Е 0. В этом случае закон сохранения энергии дает простое соотношение
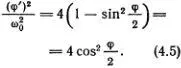
Если маятник находится в верхнем положении, т. е. φ = π или φ = -π, то его скорость равна нулю, и он может пребывать в состоянии покоя. График такого движения: φ( t ) = π при всех t , или φ( t ) = -π при всех t . На фазовой плоскости точки φ = π, φ' = 0 и φ = -π, φ' = 0 — это точки покоя (или точки равновесия). Ясно, что эти точки равновесия, в отличие от нижней точки равновесия маятника, неустойчивы. Если чуть-чуть увеличить полную энергию, скажем, резким движением слегка толкнуть маятник, то он начнет совершать вращательное движение. Если уменьшить полную энергию, скажем, медленно сдвинуть и отпустить маятник, то он начнет совершать колебательные движения с амплитудой, близкой к π. В обоих случаях он далеко уходит от положения равновесия. Если бы мы проделали то же самое в нижнем положении равновесия, то ясно, что маятник начал бы колебаться около этого положения с небольшой амплитудой. Точка φ = 0, φ' = 0 на фазовой плоскости — устойчивая точка покоя.
При Е = 4 Е 0 возможно и другое движение маятника . Пусть при t = 0 угловая скорость φ' равна 2ω 0. Тогда из формулы (4.3) следует, что Е/E 0= 4, и маятник движется к верхней точке так, что его скорость в положении φ равна
φ' = 2ω 0cos φ/2 . (4.6)
Чем ближе φ к π, тем меньше скорость. Если угол отклонения очень близок к π, то удобно обозначить малый угол отклонения π - φ через 2α. Тогда cos (φ/2) = cos (π/2 - α) = sin α  α. Скорость изменения угла φ равна, очевидно, -2α'. Поэтому между α' и α при малом значении угла α есть простое соотношение
α. Скорость изменения угла φ равна, очевидно, -2α'. Поэтому между α' и α при малом значении угла α есть простое соотношение
α'  -ω 0α, (4.7)
-ω 0α, (4.7)
которое следует из (4.6) при малом значении π - φ.
В уравнении (4.7) можно узнать уравнение, описывающее радиоактивный распад, если считать α( t ) массой нераспавшегося к моменту времени t радиоактивного вещества. Решение уравнения радиоактивного распада хорошо известно:
α( t ) = α 0 е - ω 0 t .
Здесь α 0— начальное количество вещества, α(0) = α 0, основание натуральных логарифмов е = 2,718281828... В Приложении показано, как получить это решение чисто геометрически. Здесь нам важно лишь то, что оно при возрастании t быстро убывает, но никогда не обращается в нуль. Это означает, что маятник ни за какое конечное время не придет в верхнее положение равновесия. Для понимания качественного характера движения нам больше ничего и не нужно. Можно сразу нарисовать приблизительный вид графика движения с энергией Е = 4 Е 0. Правда, наши рассуждения относились лишь к положительным значениям времени t , но левую часть кривой легко построить, вспомнив, что маятник качается совершенно симметрично относительно нижнего положения (для сравнения тонкой кривой изображено колебательное движение с энергией, меньшей 4 Е 0). Эта симметрия приводит к тому, что энергетическая и фазовая диаграммы симметричны относительно вертикальной оси. Если в какой-то момент t маятник находится в положении φ( t ), то в момент - t он находился в положении φ(- t ) = -φ( t ) (напомним, что время отсчитывается так, что в момент t = 0 маятник находится в нижнем положении, см. рис. 4.10).
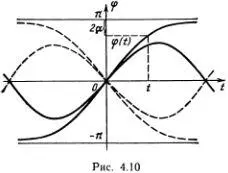
Фазовая диаграмма симметрична и относительно горизонтальной оси. Это значит, что всякому качанию слева направо, когда φ возрастает, соответствует точно такое же качание справа налево. График такого движения изображается кривой, симметричной относительно вертикальной оси (эти кривые изображены на рис. 4.10 штриховой линией).
Читать дальше

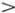 4, и даже при максимальном значении потенциальной энергии 4 sin 2(φ/2) (при φ = π потенциальная энергия равна 4) кинетическая энергия (φ') 2/ω 0 2не равна нулю, и маятник проскакивает верхнюю точку. Теперь он совершает не колебательное, а вращательное движение.
4, и даже при максимальном значении потенциальной энергии 4 sin 2(φ/2) (при φ = π потенциальная энергия равна 4) кинетическая энергия (φ') 2/ω 0 2не равна нулю, и маятник проскакивает верхнюю точку. Теперь он совершает не колебательное, а вращательное движение.
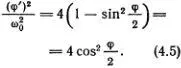
 α. Скорость изменения угла φ равна, очевидно, -2α'. Поэтому между α' и α при малом значении угла α есть простое соотношение
α. Скорость изменения угла φ равна, очевидно, -2α'. Поэтому между α' и α при малом значении угла α есть простое соотношение











