*) Гюйгенс получил ее другим способом, основанным на открытом им свойстве изохронности колебаний циклоидального маятника, а рассуждения, приведенные выше, использовал для определения ускорения точки, движущейся по окружности (о циклоидальном маятнике см. в книге: Гиндикин С. Г. Рассказы о физиках и математиках. — 2-e изд. — М.: Наука, 1984. Библиотечка «Квант», вып. 14).
Основным для Галилея был найденный опытным путем закон равной продолжительности качаний маятников одинаковой длины, или изохронизм их колебаний (от греч. «изос» — равный, «хронос» — время). Для дальнейших рассуждений он использовал открытый им закон свободного падения и связь движения по наклонной плоскости со свободным падением. Если слегка модернизировать рассуждения Галилея, как это сделал Л. И. Мандельштам в своих замечательных «Лекциях по колебаниям», прочитанных в 1930 г., то можно даже получить формулу, похожую на формулу Гюйгенса.
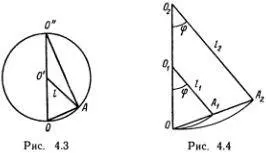
Заменим движение грузика по дуге АО из состояния покоя свободным движением по хорде АО (рис. 4.3). Тогда время t, затраченное на это падение, равно времени свободного падения из О" в О . Это следует из известного Галилею факта, что ускорение движения по катету прямоугольного треугольника относится к g, как длина ОА относится к длине ( OO" ) = 2 l (сообразите, почему). Так как 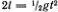 , то четверть периода колебаний равна
, то четверть периода колебаний равна 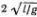 , а полный период
, а полный период 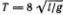 . Галилей рассуждал несколько иначе и ограничился утверждением о пропорциональности времен скатывания по хорде АО и движения маятника по дуге ОА времени свободного падения по вертикали О"О , откуда он и вывел пропорциональность этого времени квадратному корню из длины маятника.
. Галилей рассуждал несколько иначе и ограничился утверждением о пропорциональности времен скатывания по хорде АО и движения маятника по дуге ОА времени свободного падения по вертикали О"О , откуда он и вывел пропорциональность этого времени квадратному корню из длины маятника.
Подлинное рассуждение Галилея легко понять из рис. 4.4. Время скатывания грузика по наклонной плоскости ОА 1А 2 пропорционально квадратному корню из длины (( OA 1 ) для первого маятника и ( ОА 2 ) для второго). Эти длины ОА 1 и ОА 2 пропорциональны длинам маятников ( O 1O ) = l 1и ( O 2O ) = l 2 . С учетом закона свободного падения отсюда следует, что Т пропорционально 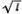 для подобных колебаний (т. е. с одинаковым максимальным углом отклонения φ).
для подобных колебаний (т. е. с одинаковым максимальным углом отклонения φ).
Используя изохронность, доказываем, что это верно для любых колебаний.
Для малых колебаний рассуждения Галилея совершенно правильны. Малые колебания действительно изохронны. Как мы теперь понимаем, изохронность прямо следует из линейности . Действительно, если колебание с единичной амплитудой определяется функцией φ = sin (ω 0 t ), то колебание с амплитудой φ M , в силу линейности, можно найти простым умножением на φ M . Это и значит, что период остается неизменным. Остальная часть рассуждения Галилея особенно интересна тем, что в ней содержится намек на использование соображений о подобном поведении подобных систем. В ясном виде принцип подобия впервые сформулировали Ньютон и Гук. Это настолько полезная вещь, что стоит сделать небольшое отступление.
Малое с великим схоже,
Хоть и разнится на вид.
В. Гёте
Принцип подобия Ньютона—Гука оставался в забвении более ста лет, пока его не возродил Фурье в упоминавшейся выше работе «Аналитическая теория теплоты». Он ввел очень важные понятия размерности физической величины и принцип однородности по размерностям . Измерение всех механических величин сводится к измерению нескольких основных, в качестве которых обычно берут длину (размерность L ), время (размерность Т ) и массу (размерность М ). Остальные величины назовем « производными ».
Так, измерение площади сводится к измерению длин. Чтобы измерить площадь прямоугольника S , мы измеряем длины его сторон и перемножаем их. Если обе стороны умножить на одно и то же число с , то площадь умножится на с 2. Это означает, что размерность площади равна квадрату размерности длины, и этот факт можно записать с помощью « формулы размерности » [ S ] = L 2. Формула размерности для S говорит нам, что площади любых фигур умножаются на одно число с 2, если все линейные размеры умножить на с (например, при фотоувеличении). Если бы мы не знали, как вычислить площадь круга радиуса R , то из формулы размерности получили бы, что S = cR 2, где c — некоторое число, о котором формула размерности ничего не говорит. Измерив c для какого-нибудь круга, мы с помощью формулы размерности будем знать, как вычислить площадь любого круга.
Читать дальше

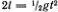 , то четверть периода колебаний равна
, то четверть периода колебаний равна 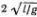 , а полный период
, а полный период 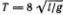 . Галилей рассуждал несколько иначе и ограничился утверждением о пропорциональности времен скатывания по хорде АО и движения маятника по дуге ОА времени свободного падения по вертикали О"О , откуда он и вывел пропорциональность этого времени квадратному корню из длины маятника.
. Галилей рассуждал несколько иначе и ограничился утверждением о пропорциональности времен скатывания по хорде АО и движения маятника по дуге ОА времени свободного падения по вертикали О"О , откуда он и вывел пропорциональность этого времени квадратному корню из длины маятника.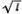 для подобных колебаний (т. е. с одинаковым максимальным углом отклонения φ).
для подобных колебаний (т. е. с одинаковым максимальным углом отклонения φ).











