Чтобы подступиться к решению нелегкой задачи о движениях маятника, рассмотрим сначала малые колебания, когда угол настолько мал, что можно положить sin φ  φ. Уравнение теперь становится линейным (это и есть линеаризация!):
φ. Уравнение теперь становится линейным (это и есть линеаризация!):

, и можно угадать (или вспомнить!) его решение φ = φ M (ω 0 t ) *), которое равно нулю при t = 0. Благодаря линейности уравнения максимальное значение угла φ M формально может быть произвольным числом, но мы, конечно, должны помнить, что при больших значениях φ M наше приближение не годится. Поэтому число φ M должно быть таким, что sin φ M  φ M .
φ M .
*) для этого достаточно вспомнить правило дифференцирования тригонометрических функций. Ниже это движение будет построено другим, геометрическим способом.
Этим решением, разумеется, не исчерпывается все множество решений. Мы заранее предположили, что φ(0) = 0, и этим отбросили, например, решение φ = cos (ω 0 t ), которое тоже легко угадать. Пользуясь линейностью, теперь можно найти и общее решение, складывая sin (ω 0 t ) и cos (ω 0 t ), умноженные на произвольные амплитуды. Ясно, что этим способом получается любое колебание, так как первое решение позволяет получить любое значение скорости в начальный момент, а второе — задать любое начальное положение.
Самое общее малое колебание можно получить и другим способом, понимание которого очень полезно. Заметим, что движение φ = φ M sin(ω 0 t ) можно наблюдать, пустив другие часы отсчитывать время в момент t 0 (по старым часам). При новом отсчете времени то же самое движение будет выглядеть как φ = φ M sin[ω 0 (t + t 0 ) ].
Нетрудно проверить, что это решение при любых t 0 удовлетворяет уравнению 4.1. Отсюда следует, что если движение φ = φ M sin(ω 0 t ) возможно, то и движение φ = φ M sin[ω 0 (t + t 0 ) ] также возможно. А это движение уже самое общее, поскольку подбором φ M и t 0можно задать любые начальные значения скорости и положения.
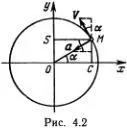
Решение уравнения для малых колебаний можно найти совсем простым способом. Достаточно вспомнить геометрическое определение тригонометрических функций и закон движения материальной точки по окружности. Пусть точка М движется по окружности единичного радиуса с постоянной скоростью V = ω 0(рис. 4.2). Скорость V направлена по касательной, и ее проекция на ось Оу равна ω 0cos α , где α = ω 0 t (радиан). Точка S совершает гармоническое движение, длина отрезка ( OS ) = sin ω 0 t , и ее скорость v равна проекции скорости V на ось Оу , т. е. v = ω 0cos(ω 0 t) . Полное ускорение α направлено к центру и равно 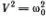 (радиус окружности равен 1). Ускорение точки S равно проекции ускорения а на ось Оу , т. е.
(радиус окружности равен 1). Ускорение точки S равно проекции ускорения а на ось Оу , т. е. 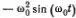 . Таким образом, ускорение точки S равно
. Таким образом, ускорение точки S равно 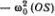 . Если взять ( OS ) = φ, получим φ" =
. Если взять ( OS ) = φ, получим φ" = 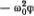 . Обозначив
. Обозначив  , находим, что φ = sin(ω 0 t ) есть решение линейного уравнения для малых колебаний маятника. Заодно вспомним, что период колебаний Т совпадает с временем полного оборота точки М по окружности, т. е. равен
, находим, что φ = sin(ω 0 t ) есть решение линейного уравнения для малых колебаний маятника. Заодно вспомним, что период колебаний Т совпадает с временем полного оборота точки М по окружности, т. е. равен 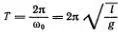 .
.
Эта формула, хорошо известная из школьного курса физики, была впервые найдена Гюйгенсом *). С точностью до числового множителя она, по-видимому, была известна уже Галилею. История ее открытия интересно и подробно описана в упоминавшейся в книге С. Г. Гиндикина, но с одним утверждением, сделанным в ней, можно поспорить. Там сказано (с. 39): «Галилей обнаруживает связь между длиной маятника и частотой его колебаний: квадраты периодов колебаний относятся как длины. Вивиани пишет, что Галилей получил этот результат, «руководствуясь геометрией и своей новой наукой о движении», но никто не знает, каким мог быть теоретический вывод. Быть может, все же Галилей подметил закономерность экспериментально?» Принять это предположение было бы несправедливостью по отношению к Галилею. На опыте он лишь подметил зависимость периода от длины, но закон пропорциональности периода квадратному корню из длины нашел с помощью довольно остроумных рассуждений, которые представляют не только исторический интерес.
Читать дальше

 φ. Уравнение теперь становится линейным (это и есть линеаризация!):
φ. Уравнение теперь становится линейным (это и есть линеаризация!):

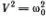 (радиус окружности равен 1). Ускорение точки S равно проекции ускорения а на ось Оу , т. е.
(радиус окружности равен 1). Ускорение точки S равно проекции ускорения а на ось Оу , т. е. 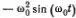 . Таким образом, ускорение точки S равно
. Таким образом, ускорение точки S равно 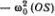 . Если взять ( OS ) = φ, получим φ" =
. Если взять ( OS ) = φ, получим φ" = 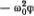 . Обозначив
. Обозначив  , находим, что φ = sin(ω 0 t ) есть решение линейного уравнения для малых колебаний маятника. Заодно вспомним, что период колебаний Т совпадает с временем полного оборота точки М по окружности, т. е. равен
, находим, что φ = sin(ω 0 t ) есть решение линейного уравнения для малых колебаний маятника. Заодно вспомним, что период колебаний Т совпадает с временем полного оборота точки М по окружности, т. е. равен 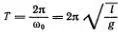 .
.










