*) Как мы уже говорили, «досадным» исключением оставалась лишь гидродинамика.
Почему линейность так упрощает решение задачи? Проще всего это понять на простых примерах. Рассмотрим уравнение ах + y = 0, решения которого — это пары чисел (x, у), при подстановке которых оно обращается в тождество. Ясно, что всякое решение можно записать в виде (х 0, -ax 0), где x 0— произвольное число. Если изобразить решения точками на плоскости, то все решения лежат на прямой ОА, проходящей через точки О = (0, 0) и А = (1, -a). Если мы знаем только одно решение А, то, пользуясь линейностью, можно получить все решения умножением на произвольное число: х 0А = (х 0, -aх 0). Математик скажет, что совокупность всех решений этого уравнения образует линейное одномерное многообразие . Для определения всех его точек достаточно задать одну точку, отличную от О (0, 0), например, А = (1, -a). Если 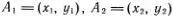 — две точки этого многообразия, то точка А 3= c 1A 1+ с 2А 2=
— две точки этого многообразия, то точка А 3= c 1A 1+ с 2А 2= 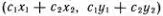 , при любых с 1и с 2тоже принадлежит этому многообразию (т. е. точка А 3тоже лежит на прямой ОА).
, при любых с 1и с 2тоже принадлежит этому многообразию (т. е. точка А 3тоже лежит на прямой ОА).
Точно также можно найти все решения уравнения ах + by + z = 0, т. е. тройки чисел (x, y, z), при подстановке которых уравнение обращается в тождество. Можно убедиться, что достаточно знать два решения, например, 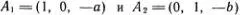 , а все остальные получаются их линейными комбинациями , т. е.
, а все остальные получаются их линейными комбинациями , т. е. 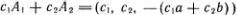 . Это пример двумерного линейного многообразия . Геометрически можно изобразить его как плоскость в трехмерном пространстве (попробуйте проверить эти утверждения и нарисовать такую плоскость).
. Это пример двумерного линейного многообразия . Геометрически можно изобразить его как плоскость в трехмерном пространстве (попробуйте проверить эти утверждения и нарисовать такую плоскость).
Рассмотрим теперь более близкий к физике пример колебаний грузика на пружине. Отклонение грузика от положения равновесия x(t) подчиняется уравнению Ньютона 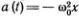 , где а(t) — ускорение грузика в момент t , ω 0— круговая частота, ω 0 = 2π/ Т , а Т — период колебаний грузика. Если x 1(t) и x 2(t) — два решения этого уравнения, описывающие какие-то два движения, то и любая их линейная комбинация
, где а(t) — ускорение грузика в момент t , ω 0— круговая частота, ω 0 = 2π/ Т , а Т — период колебаний грузика. Если x 1(t) и x 2(t) — два решения этого уравнения, описывающие какие-то два движения, то и любая их линейная комбинация 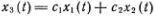 — тоже решение (т. е. х 3(t) — возможное движение) *). Совокупность всех решений также образует линейное многообразие.
— тоже решение (т. е. х 3(t) — возможное движение) *). Совокупность всех решений также образует линейное многообразие.
*) Так как ускорение a(t) линейно зависит от x(t) .
Рассмотрим два движения: x 1(t) = cos(ω 0 t ) и x 2(t) = sin(ω 0 t ). Взяв 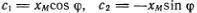 , можно написать произвольную линейную комбинацию из x 1 и x 2 :
, можно написать произвольную линейную комбинацию из x 1 и x 2 : 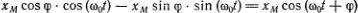 . Так получается самое общее выражение для отклонений грузика при колебаниях с амплитудой х M и фазой φ. По аналогии с рассмотренными нами алгебраическими уравнениями можно сказать, что линейное многообразие возможных колебаний двумерно. Каждое колебание грузика можно представить точкой на плоскости ( с 1, с 2 ), и эти точки также образуют линейное многообразие.
. Так получается самое общее выражение для отклонений грузика при колебаниях с амплитудой х M и фазой φ. По аналогии с рассмотренными нами алгебраическими уравнениями можно сказать, что линейное многообразие возможных колебаний двумерно. Каждое колебание грузика можно представить точкой на плоскости ( с 1, с 2 ), и эти точки также образуют линейное многообразие.
Над этими простыми примерами стоит как следует подумать. Важно понять, во-первых, что любое колебание грузика можно представить в виде суммы двух линейно независимых, т. е. не выражающихся друг через друга в виде линейных комбинаций колебаний x 1 = cos(ω 0 t ) и x 2 = sin(ω 0 t ) (вместо этих можно взять и другие линейно независимые решения). Наоборот, пусть известны два возможных колебания x 1(t) и x 2(t) , отношение которых не постоянно, — такие колебания будут линейно независимыми . Тогда любое другое движение можно получить, подобрав подходящие числа с 1 и с 2 и складывая колебание с 1x 1(t) с с 2x 2(t) . Важно, что при этом не нужно знать даже само уравнение. Достаточно иметь два независимых колебания и знать, что выполнен принцип линейности или принцип сложения колебаний.
Если линейности нет, то все выглядит гораздо сложнее. Возьмем самое простое уравнение y 2+ аx 2= 0. Сразу ясно, что многообразие решений (x, у) будет иметь совершенно разный вид при разных знаках а . При а 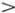 0 оно состоит из единственной точки О = (0, 0). При а = 0 — это точки, лежащие на оси Оx , т. е. точки ( x 0 , 0), где x 0 — любое число. Если же а
0 оно состоит из единственной точки О = (0, 0). При а = 0 — это точки, лежащие на оси Оx , т. е. точки ( x 0 , 0), где x 0 — любое число. Если же а 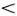 0, то все решения имеют вид или
0, то все решения имеют вид или 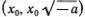 , или
, или 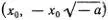 , т. е. лежат либо на прямой ОА , либо на прямой ОB (рис. 3.9).
, т. е. лежат либо на прямой ОА , либо на прямой ОB (рис. 3.9).
Читать дальше

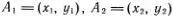 — две точки этого многообразия, то точка А 3= c 1A 1+ с 2А 2=
— две точки этого многообразия, то точка А 3= c 1A 1+ с 2А 2= 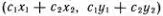 , при любых с 1и с 2тоже принадлежит этому многообразию (т. е. точка А 3тоже лежит на прямой ОА).
, при любых с 1и с 2тоже принадлежит этому многообразию (т. е. точка А 3тоже лежит на прямой ОА).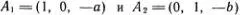 , а все остальные получаются их линейными комбинациями , т. е.
, а все остальные получаются их линейными комбинациями , т. е. 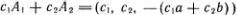 . Это пример двумерного линейного многообразия . Геометрически можно изобразить его как плоскость в трехмерном пространстве (попробуйте проверить эти утверждения и нарисовать такую плоскость).
. Это пример двумерного линейного многообразия . Геометрически можно изобразить его как плоскость в трехмерном пространстве (попробуйте проверить эти утверждения и нарисовать такую плоскость).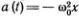 , где а(t) — ускорение грузика в момент t , ω 0— круговая частота, ω 0 = 2π/ Т , а Т — период колебаний грузика. Если x 1(t) и x 2(t) — два решения этого уравнения, описывающие какие-то два движения, то и любая их линейная комбинация
, где а(t) — ускорение грузика в момент t , ω 0— круговая частота, ω 0 = 2π/ Т , а Т — период колебаний грузика. Если x 1(t) и x 2(t) — два решения этого уравнения, описывающие какие-то два движения, то и любая их линейная комбинация 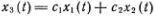 — тоже решение (т. е. х 3(t) — возможное движение) *). Совокупность всех решений также образует линейное многообразие.
— тоже решение (т. е. х 3(t) — возможное движение) *). Совокупность всех решений также образует линейное многообразие.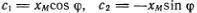 , можно написать произвольную линейную комбинацию из x 1 и x 2 :
, можно написать произвольную линейную комбинацию из x 1 и x 2 : 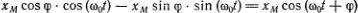 . Так получается самое общее выражение для отклонений грузика при колебаниях с амплитудой х M и фазой φ. По аналогии с рассмотренными нами алгебраическими уравнениями можно сказать, что линейное многообразие возможных колебаний двумерно. Каждое колебание грузика можно представить точкой на плоскости ( с 1, с 2 ), и эти точки также образуют линейное многообразие.
. Так получается самое общее выражение для отклонений грузика при колебаниях с амплитудой х M и фазой φ. По аналогии с рассмотренными нами алгебраическими уравнениями можно сказать, что линейное многообразие возможных колебаний двумерно. Каждое колебание грузика можно представить точкой на плоскости ( с 1, с 2 ), и эти точки также образуют линейное многообразие.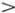 0 оно состоит из единственной точки О = (0, 0). При а = 0 — это точки, лежащие на оси Оx , т. е. точки ( x 0 , 0), где x 0 — любое число. Если же а
0 оно состоит из единственной точки О = (0, 0). При а = 0 — это точки, лежащие на оси Оx , т. е. точки ( x 0 , 0), где x 0 — любое число. Если же а 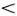 0, то все решения имеют вид или
0, то все решения имеют вид или 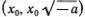 , или
, или 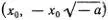 , т. е. лежат либо на прямой ОА , либо на прямой ОB (рис. 3.9).
, т. е. лежат либо на прямой ОА , либо на прямой ОB (рис. 3.9).










