Уолтер Левин - Глазами физика. От края радуги к границе времени

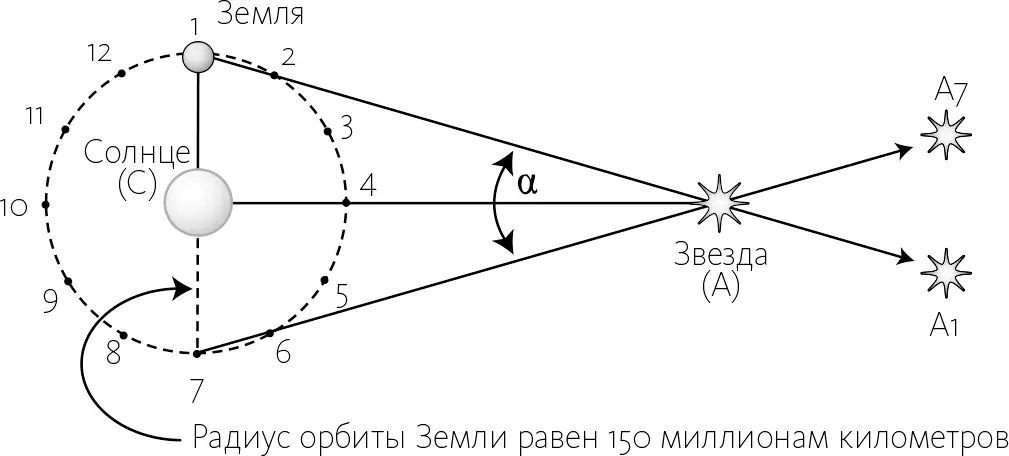
Предположим, вы наблюдаете звезду А в момент, когда Земля, двигаясь по орбите вокруг Солнца (С), находится в положении 1. В этом случае вы видите звезду проецируемой на фон (очень удаленный) в направлении A1. Если же вы наблюдаете ту же звезду шесть месяцев спустя (с позиции 7), то увидите ее в направлении A7. Угол, обозначенный как α, наибольший из всех возможных углов параллакса. Если произвести аналогичные замеры с позиций 2 и 8, 3 и 9, 4 и 10, углы параллакса всегда будут меньше, чем α. В гипотетическом варианте наблюдений из пунктов 4 и 10 (гипотетическом, потому что с позиции 10 звезду наблюдать невозможно, ибо мешает Солнце) угол параллакса вообще был бы равен нулю. А теперь посмотрите на треугольник, образуемый точками 1А7. Мы знаем, что расстояние 1–7 составляет 300 миллионов километров; нам также известно, что угол равен α. Следовательно, теперь можно без труда рассчитать расстояние CA (математика уровня средней школы).

Несмотря на то что углы параллакса, измеренные в разные полугодовые периоды, отличаются друг от друга, астрономы говорят о конкретном параллаксе звезды, под которым подразумевают величину, равную половине самого большого угла параллакса. Так, если максимальный угол параллакса составляет 2,00 угловые секунды, то параллакс звезды будет равен 1,00 угловой секунде, а расстояние до нее в этом случае составит 3,26 световых года (хотя на самом деле звезд, столь близких к Земле, не существует). Чем меньше параллакс, тем больше расстояние. Если параллакс равен 0,10 угловой секунды, расстояние до нее будет 32,6 световых года. Самая близкая к Солнцу звезда – Проксима Центавра. Ее параллакс – 0,76 угловой секунды; таким образом, от Земли ее отделяет около 4,3 световых года.

Чтобы лучше понять, насколько малые изменения в положениях звезд приходится измерять астрономам, для начала следует разобраться, что же представляет собой угловая секунда. Представьте себе огромный круг, нарисованный в ночном небе через зенит (направление, указывающее непосредственно вверх) вокруг Земли. Поскольку это круг, то в нем, естественно, 360 градусов. Так вот, каждый градус делится на 60 угловых минут, а каждая угловая минута, в свою очередь, – на 60 угловых секунд. Таким образом, в полном круге 1 296 000 угловых секунд. Как видите, угловая секунда – величина крайне маленькая.

Вот еще один способ наглядно представить себе, насколько она мала. Если взять монету в десять центов и поместить ее примерно на расстоянии 3,5 километра от вас, то ее диаметр будет составлять одну угловую секунду. Или еще. Каждый астроном знает, что диаметр Луны равен около половины градуса, или 30 угловых минут. Это называется угловым размером Луны. Так вот, если бы вы умудрились нарезать Луну на 1800 одинаково тонких ломтиков, ширина каждого из них равнялась бы одной угловой секунде.

Учитывая, насколько малы размеры углов параллакса, которые должны измерять астрономы для определения расстояний до звезд, отлично понимаешь, как важна для них степень точности данных измерений.

По мере появления специального оборудования, позволяющего астрономам производить все более точные измерения, их оценки расстояний до звезд порой весьма существенно менялись. В начале XIX века Томас Хендерсон измерил параллакс самой яркой звезды на небе, Сириуса, и определил, что он равен 0,23 угловой секунды с погрешностью около четверти угловой секунды. Иными словами, по оценке Хендерсона, верхний предел параллакса Сириуса составляет около половины угловой секунды, а это означало, что данная звезда находится от нас не ближе чем на расстоянии 6,5 световых года. Для 1839 года это был очень важный вывод. Но спустя полвека Дэвид Гилл определил, что параллакс Сириуса равен 0,370 угловой секунды с погрешностью плюс-минус 0,010 угловой секунды. Измерения Гилла не противоречили данным Хендерсона, но были намного точнее, потому что их погрешность была в двадцать пять раз меньше. При параллаксе 0,370 ± 0,010 угловой секунды расстояние до Сириуса становится равным 8,81 ± 0,23 световых года, что существенно больше шести с половиной световых лет!

В 1990-е годы спутник для высокоточных определений параллаксов с названием (подозреваю, создатели долго с ним экспериментировали, пока не подогнали под имя древнегреческого астронома Гиппарха) Hipparcos (акроним от High Precision Parallax Collecting Satellite) измерил параллаксы более ста тысяч звезд (и, следовательно, расстояния до них) с относительной погрешностью всего около одной тысячной угловой секунды. Разве это не невероятно? Помните, как далеко должна находиться монетка, чтобы ее диаметр составлял одну угловую секунду? А чтобы он был равен тысячной доле угловой секунды, монетка должна находиться за 3,5 тысячи километров от наблюдателя.