Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

Итак, есть некий порт A. От него со скоростью v удаляется некий корабль B . Естественно, скорость корабля определена относительно воды. По неким причинам связь между портом и кораблем поддерживается следующим не слишком удобным способом.

Через промежутки времени Δ t начальник порта отправляет на корабль посыльные катера.

Капитан корабля делает то же самое. Он также отправляет катера в порт через интервалы Δ t . Скорость катеров относительно воды обозначим c . Естественно, c > v . Иначе ни один катер из порта не попал бы на корабль.

Требуется узнать, какой интервал времени между двумя последующими приемами катеров из порта пройдет на корабле и каков интервал между приходами катеров в порту.

Найдем время, которое тратит катер, чтобы добраться из порта до корабля.

Если в момент отправления первого катера расстояние до корабля было a , то время пути катера определяется очевидным равенством:

S = c · t 1 пут = a + vt 1 пут, и отсюда:

t 1 пут = a /( c – v ).

В момент, когда отправится следующий катер, корабль будет находиться уже на расстоянии a + Δ t · v, и время пути этого катера, естественно, равно

t 2 пут = ( a + Δ t · v )/( c - v )

Если первый катер был отправлен в момент t 0, а второй соответственно в момент t 0 + Δ t , то времена их прибытия на корабль соответственно:

t 1 прибыт = t 0 + a/ c – v ;

t 2 прибыт = t 0 + Δ t + a + Δ t · v / c – v ;

А интервал времени между приемами катеров, очевидно, равен:

Δ t приема = t 2 прибыт – t 1 прибыт = Δ t (1 + v / c – v ).

Или если ввести β = v / c :

Δ t приема = Δ t (1 + β/ 1 – β) = Δ t / (1 – β).

Как видите, интервал между двумя приемами катеров больше, чем интервал между моментами их отправления. Это, конечно, совершенно понятно, потому что второй катер находился в худших условиях — ему нужно пройти бóльший путь, чем предыдущему.

Обратим теперь внимание, что в выражение для Δ t приемане входит величина a — начальное расстояние корабля от порта. Иными словами, для любой пары катеров, следующих друг за другом, растяжение интервала между их прибытием на корабль определяется только отношением

( v / c ).

Если корабль не удаляется, а приближается, достаточно изменить знак скорости корабля. Характер решения не изменится. (Надеюсь, что в этом читатели могут убедиться самостоятельно.)

Итак, Δ t приема = Δ t / (1±β).

Знаки – и + соответствуют удалению и приближению корабля.

Если ввести новую характеристику — частоту отправления и приема катеров, а она, естественно, определится как ν = 1/ Δ t , то мы получим:

ν приема = ν отправл(1±β).

Рассмотренный пример совершенно точно показывает, как изменится частота звуковых волн, если источник покоится относительно атмосферы, а приемник движется.

Если бы была правильна теория неувлекаемого эфира, точно так же должно было обстоять и с электромагнитными волнами.

Полагаю, что читатели смогут сами определить частоту приема в порту катеров, посланных с корабля, и получить формулу:

ν приема = ν отправл/(1±β).

Здесь + соответствует приближению, а – удалению корабля.

Как видите, хотя качественно в обоих случаях частота меняется одинаково, количественно должны наблюдаться разные результаты в зависимости от того, источник или приемник движутся относительно эфира, даже если скорость их относительно эфира одинакова [47] .

Часто приходится читать, что, слушая рев сирены электропоезда, проезжающего мимо наблюдателя на полотне дороги, легко можно непосредственно наблюдать эффект Допплера.

Должен заметить, что, очевидно, это возможно лишь для людей с очень развитым слухом. Обычно же фиксируется не изменение частоты, а изменение громкости (интенсивности). Поэтому наблюдатели без особых музыкальных данных и несколько «испорченные» образованием отождествляют кривую изменения интенсивности звука с теоретически предсказанным изменением частоты и приходят к выводу, что кривая для изменения частоты в акустическом эффекте Допплера имеет примерно такой вид.

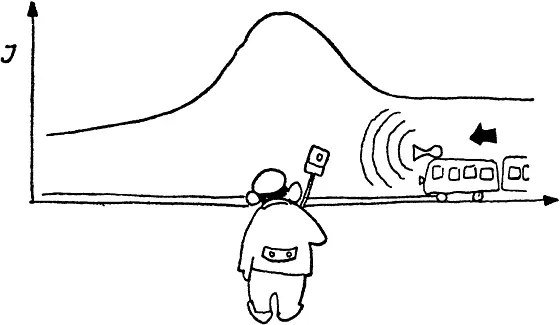
На самом же деле по оси ординат здесь откладывается интенсивность, а не частота.