Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

Схема рассуждений должна быть примерно такой. Пусть дана какая-то система отсчета: обозначим ее для удобства, скажем, буквой K . В ней мы умеем описывать движение тел и предметов при помощи законов Ньютона. Так, если изучаемое тело изолировано и свободно, оно в нашей системе либо покоится, либо движется с постоянной скоростью V .

Но вот есть другая система отсчета, скажем K 1, которая движется относительно К равномерно и прямолинейно с известной нам скоростью v .

При этих условиях мы должны научиться определять положение изучаемого тела в новой системе отсчета. Ведь чтобы ответить на вопрос, каков характер движения тела в новой системе K 1, надо знать его координаты в этой системе в любой момент времени.

Иными словами, нужно найти закон перехода от одной системы отсчета к другой.

Найти этот закон довольно просто в самом общем случае, но мы рассмотрим наипростейший, а именно: во-первых, когда система K 1движется с постоянной скоростью вдоль оси x системы K ; и во-вторых, когда скорость нашего свободного тела V направлена также вдоль оси x системы K .

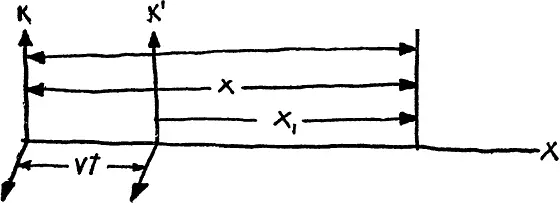
Тогда, если в момент t 0 = 0 системы отсчета совпадали, то за время t начало координат системы K 1«уедет» на расстояние S = vt . Как видно из чертежа, координаты тела в новой системе можно найти, зная координаты в старой системе и используя очевидные соотношения:

x 1 = х – vt ;

у 1 = у ;

z 1 = z .

Прошу поверить на слово, что если рассматривать общий случай (скорости V и v направлены не вдоль осей и не совпадают по направлениям), наши выводы останутся правильными.

Но вернемся к примеру. В каждый данный момент времени в старой системе отсчета координаты нашего тела определяются соотношениями:

x = x 0 + Vt ;

y = y 0;

z = z 0.

Здесь x 0, y 0, z 0— координаты тела в начальный момент t = 0.

Вспомнив формулы для перехода от одной системы к другой, получаем:

x 1 = x 0 + (V – v ) t ;

у 1 = у 0;

z 1 = z 0.

Итак, в новой системе тело снова двигается равномерно и прямолинейно вдоль оси x 1, но уже с новой скоростью V 1 = V – v .

Иначе говоря, мы доказали, что если первый закон Ньютона справедлив в системе K , то он справедлив и в K 1.

Точно так же (хотя с формальной стороны это несколько сложнее) можно показать, что если K 1движется неравномерно или непрямолинейно относительно K , то тело, которое в K покоилось или двигалось с постоянной скоростью, в системе K 1будет двигаться уже неравномерно или непрямолинейно.

И тем не менее в наших рассуждениях есть очень существенный пробел. Когда мы переходили от одной системы отсчета к другой, мы молчаливо допускали, что время в обеих системах течет одинаково. Если внимательно проследить за выводом, то можно увидеть, что в выражении x 1 = x 0 + ( V – v ) t величина t по своему смыслу означает время, измеренное в системе K . А строго говоря, чтобы описывать движение тела в системе K 1мы должны вместо t использовать t 1, то есть время, измеренное в системе K 1. Может быть, в системе K 1к моменту определения координат тело прошло 5 минут, а в системе K только 4?! Но мы молчаливо предполагали, что t 1 = t .

Почему мы сделали это предположение?

Только потому, что повседневный опыт убеждает нас в его справедливости [21] .

Однако возникает законный вопрос, что вообще означают слова «время, измеренное в одной системе, время, измеренное в другой системе», какой смысл вкладывается в эти понятия?

Какой физический процесс соответствует символам t 1и t , а, кстати, заодно и x 1и x ?

Символы — это ведь не более чем символы. Они получают жизнь только тогда, когда мы однозначно определим, как именно можно отыскать те физические величины, которые они описывают.

Таким образом, вопрос о переходе от одной системы отсчета к другой возвращает нас снова к проблеме измерения времени.

Поэтому логично и естественно дать именно сейчас рецепт для измерения и координат и времени в данной системе.