Константин Ефанов - Аппараты с перемешивающими устройствами

Метод конечных объемов обеспечивает для исходный дифференциальных уравнений Навье-Стокса выполнение законов сохранения в интегральной форме, то есть обладает свойством консервативности [12,с.51]. Законы сохранения могут быть записаны для различных величин, например, массы, импульса и др.

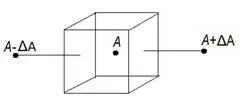
Скорость накопления величины А в ячейке равна сумме конвективного и диффузионного притока в единицу времени [12,с.52]. По граням смежных ячеек решение интеграла должно быть одинаковым.

__

Химическая гидродинамика

К уравнениям, описывающим движение потока без химических реакций, добавляется описание химической кинетики методами, описанной в дифференциальных уравнениях химической гидродинамики. Уравнения химической гидродинамики приведены в работах [34], [35].

Решая численными методами совместно систему уравнений из дифференциальных уравнений вычислительной гидродинамики для турбулентного течения и дифференциальных уравнений химической гидродинамики, получают решение для турбулентного потока, в котором протекают химические процессы.

__

Академик Колмогоров А.Н. в работе [17] описал единственно верно модель структуры турбулентного потока. В этой же работе отмечается, что нобелевский лауреат, академик Ландау Л.Д. высказался о корректности предложенной Колмогоровым А.Н. модели. Согласно этой модели происходит передача энергии от вихрей макромасштаба более мелким и до колмогоровского масштаба. На колмогоровском масштабе энергия тратится на вязкое трение. Колмогоровский масштаб по сути совпадает с элементарным масштабом (см. выше), описанным вокруг произвольно взятой точки внутри потока. Очевидно, что корректная постановка численного расчета состоит в расчете мелких масштабов с переходом к макроскопическому масштабу, являющимся интегральным в численном расчете. По методу DNS напрямую решается система уравнений Навье-Стокса.

Для учета протекания химических реакций необходимо решаемую численным методом систему уравнений дополнить уравнениями химической гидродинамики.

__

Проблема решения уравнений Навье-Стокса рассмотрена Ефановым К.В. в работе [18] и возможно, что решена (попытка решения проблемы как физиком, а не как математиком).

В монографии подробно приведена теория расчета валов на резонанс по теории колебаний и приведена теория расчета на резонанс методом конечных элементов.

Расчеты на резонанс следует выполнять в специальных компьютерных программных пакетах, а теорию расчета необходимо знать для глубокого понимания физики процесса и для выполнения расчета а также конструирования вала.

Предложен подход по выбору мешалки, по которому по геометрии аппарата предполагается структура потока, а затем под эту структуру выбирается мешалка. Такой подход является обоснованным технически по сравнению с подбором мешалок на основе простого сравнения их выходных данных по структуре потока.

Приведен технологический расчет аппарата с мешалкой, снабженного теплообменным устройством в виде рубашки.

Приведена теория идеальных реакторов и теория вычислительных методов гидродинамики.

Критериальные методики расчета имеют меньшее физическое обоснование по сравнению с прямым решением уравнений гидродинамики.

Структура потока на основе решения уравнений гидродинамики имеет большее физическое обоснование по сравнению с моделями идеальных реакторов и учета в них неидеальности.

Расчет процессов перемешивания следует выполнять численными методами в специальных программных пакетах

1. Васильцов Э.А., Ушаков В.Г. Аппараты для перемешивания жидких сред: Справочное пособие. – Л.: Машиностроение, 1979. – 272 с.

2. Лунц Е.Б. Упругие колебания. – М.: Изд-во МАИ, 1935. – 182 с.

3. Яблонский А.А., Норейко С.С. Курс теории колебаний. 3-е изд. – М.: Высш. шк, 1975. – 248 с.

4. Бабаков И.М. Теория колебаний. 3-е изд. – М.: Наука, 1968. – 560 с.

5. Беляев Н.М. Сопротивление материалов. – М.: Наука, 1965. – 303 с.

6 Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учебное пособие. В 10т. т. 6. Гидродинамика. – 3-е изд. – М.: Наука, 1986 – 736 с.

7. Кафаров В.В. Основы массопередачи. 2-е изд. – М.: Высш. шк., 1972. – 496 с.

8. Левеншпиль О. Инженерное оформление химических процессов. – М.: Химия, 1969. – 624 с.

9. Монин А.С., Яглом А.М. Статистическая гидромеханика, т.1. М. Наука. 1965. 641 с.